Ancient Egyptian mathematics

Fig.1 Ancient Egyptian mathematics. Image: Ricardo Liberato, via Wikimedia Commons.

Egypt, located around the Nile, is one of the earliest developed culture areas in the world, and established a unified country near 3200 BC. The great characteristic of the Nile is the regularity of its floods. The periodic floods would inundate the whole land, which had to be re-measured when the waters receded. Egyptian mathematics developed to make accurate measurements for the division of land. In addition, mathematics also played an important role in prediction and preparation of flood events.

Fig. 2: Rhind Mathematical Papyrus. Image: Public domain, via Wikimedia Commons.

Our main awareness of Egyptian mathematics is based on two papyri, named the Moscow Mathematical Papyrus and the Rhind Mathematical Papyrus, which are preserved in Moscow and London respectively. Why were so few documents from ancient Egypt preserved? It’s because any kind of paper doesn’t last as long as stone, clay, or some other materials. The Egyptian utilized a kind of grass as “paper”, named papyrus, which looks like reeds and grows broadly around Nile Delta. However, this paper made of grass would easily dry and crack, and the records on it were really hard to preserve. Instead, some records on stone, clay, and other materials were preserved well. A Frenchman, whose name is Bastien, spent a very long time studying this information, and he finally figured out the meaning of the words on papyrus. His findings help us to understand some applications of the old mathematics on managing civil and religious matters. Specifically, the mathematics can be used in the division of land and wages, and the calculation of amounts of bricks required to build a building. In summary, the realistic problems motivated ancient Egyptians to master arithmetic operations, a fraction method and so on. We can see the ancient Egyptians had a gift in mathematics.

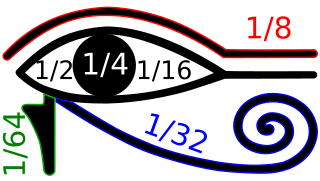
Fractions played an important role in ancient Egyptian mathematics. When an Egyptian conducted a fraction calculation, they only used as numerator. One of the famous examples in Egyptian fraction is how to divide bread. When ancient Egyptians divided nine loaves between ten people, instead of saying that each person should get 9/10 of a loaf, they would say each person should get 1/2+1/4+1/5+1/12+1/30 of a loaf. So why do they express fractions like that? According to Wikipedia, “An Egyptian fraction is the sum of distinct unit fractions, such as 1/2+1/3+1/16. That is, each fraction in the expression has a numerator equal to 1 and a denominator that is a positive integer, and all the denominators differ from each other. The value of an expression of this type is a positive rational number a/b; for instance the Egyptian fraction above sums to 43/48.[2]” We can see another bread example of how to divide only two loaves between three people. Firstly, they would divide two loaves to four halves, and each person would get half, the remaining 1/2 would be divided into three equal parts, and those three parts are divided between the three people. In the end, each person would get 1/2 plus 1/3 of 1/2, which sum is 2/3. Thus I think that they express fraction like this way because it was easy to understand for them. The Rhind Mathematical Papyrus also recorded some information about this method[3].

The origin of Egyptian mathematics was not as theory. Instead, the mathematics was applied to real life and to solve realistic problems. The beginning of mathematics was just a method to solve problems instead of a subject. Ancient Egyptian used mathematical methods to pay the workers, and found a way to pay them evenly. As time went by, people used this method and to improved this method. Thus, Egyptians studied mathematics and opened up a road for further development of mathematics. The ancient Egyptians not only invented the fraction, but also found other stuff. For example, the method of calculating area of a circle, their own calendar and so on. Those achievements brought great change and convenience for future life.

Reference:

[1]http://en.wikipedia.org/wiki/Ancient_Egyptian_mathematics

[2]http://en.wikipedia.org/wiki/Egyptian_fraction

[3]Clagett, Marshall Ancient Egyptian Science, A Source Book. Volume Three: Ancient Egyptian Mathematics (Memoirs of the American Philosophical Society) American Philosophical Society. 1999 ISBN 978-0-87169-232-0

Six Times Seven is What Again?

Mathematics is complicated. I’m pretty sure most normal people would agree with me on that opinion. There are always rules to be understood and those special circumstances in which they may not apply, things to be memorized and foundations to gain before you can move onto the next complicated thing. At the foundation of all math, though, is the need to multiply.

We all remember growing up memorizing times tables. Gross. Taking those silly timed tests over and over again until we could finally (and usually lastly) get the 6’s, 7’s and 8’s. And once that foundation is built, we start doing bigger multiplication. Hundreds times thousands and the like. Even more gross. But there are so many ways, outside of our standard multiplication algorithm, that we can visualize multiplication! We learned of one such method in class, the Egyptian Doubling method. But there are many others as well; the Russian Peasant, Sieve Multiplication, Finger Multiplication and a new fun one, Line Multiplication.

The Russian Peasant method of multiplication is very similar to the Egyptian method. The reason these 2 methods are so similar is because they are both based off of a base 2 algorithm, or a binary system. In the Egyptian method, we can see that if we break a number into its binary components and then multiply those by our other number, we can get our product. In the Russian Peasant method, the same idea is applied in a different way.

85×18 done using peasant multiplication. Image: A. Bogomolny, Peasant Multiplication from Interactive Mathematics Miscellany and Puzzles.

Let us begin by trying 85 times 18. In this method, you start as the Egyptians did with 2 columns. 85 at the top of the left column and 18 at the top of the right. In the left column you begin dividing your number in half disregarding any remainders. So 85/2 would be 42. 42/2 would be 21. 21/2 would be 10 and so on until you are left with 1. On the right side, you then double your number for as many rows that were created in the left column. Finally, you will add up the right columned numbers associated with the odd left column numbers (disregard any evens). So in this case, you will disregard 42, 10 and 2 and add 18, 72, 288 and 1152. This gives you your answer of 1530 [1].

Now notice that in this method, the odd numbers play an important role as they are the ones that you keep while you disregard the evens. The odd numbers (or the numbers which you can break up as 2k+1) show you the binary decomposition. Wherever you have a one left over (aka an odd number), that is where you will place a 1 in your binary. So 85 would be 1010101. This is how you discover which numbers to add to get to your answer.

The Sieve method is commonly known as the lattice method and originated in the Middle East in the late 1300’s [2]. This method is most similar to our multiplication method of today because it uses a base 10 algorithm much like our own system.

58×231 done using the Lattice Method. Image: Javier Rosa, via Wikipedia

Let us multiply 58 by 213 by the Sieve method. First, create a grid where your first number is listed across the top and the second down the right side with each number getting a row or column. Next, place a diagonal through each square. Then multiply your row by your column. So the first square will by 5×2, the second, 8×2 and so on. Place the tens digit of your answer in the top half of your square and the ones digit in the bottom half. Now, add down your diagonals beginning with the bottom right corner, so in this example, 4. So the next number would be 8+2+5 or 15. Make sure you only write 5 and carry your 1 to the next diagonal. Finally, you read your answer by reading the numbers down the left side and across the bottom. So our answer is 12,354 [2].

8×7 done by Finger Multiplication. Image: G. Patrick Vennebush, via Math Jokes for Mathy Folks.

Remember how I said earlier that we all hate 6’s, 7’s and 8’s? There is a method of finger multiplication that is said to have come out of Italy and was widely used during the Medieval Period that was specifically designed for all times tables 5×5 to 10×10 [3]. To begin this method, understand that every raised finger is one more than 5. Let us do 8×7, one of the most brutal of the multiplication tables. On the left hand, you will raise 3 fingers (because 8 is 3 more than 5) and 2 fingers on the right (7 is 2 more than 5). You should have a total of 5 raised fingers and 5 closed fingers, 2 closed on the left and 3 on the right [6]. You will multiply all raised fingers by 10 and then add that to the number of closed fingers on the left multiplied to the number of closed fingers on the right. In this case we have (5×10)+(2×3) or our answer, 56. Pretty nifty huh?

The final method of multiplication I wanted to talk about is one that is commonly attributed, on the internet, to the Chinese or Japanese called Line Multiplication. But as I did my research a little bit more, there are no real references to this being a Chinese or Japanese method. One person found that the earliest reference to this method was a YouTube video in 2006 but no sources have been found to accurately date it [5].

22×13 using the Line Method. Image: Francis Su, via Mudd Math Fun Facts.

Let us do 22×13 for this method. Begin by drawing diagonal lines slanting up for the tens and ones digit of your first number (2 lines, a space and then another 2 lines). Then create diagonal lines slanting down (that intersect with your first lines) for the tens and ones digit of your second number (1 line, a space and then 3 lines). You will then circle where each set of lines intersect and count the number of intersecting points and place this number just under each group. In this case we have 2 on the left side, 6 and 2 down the middle column and 6 on the right side. Add these numbers moving down your column from right to left (carrying tens when needed). Here we get 286 as our answer [4].

The one thing that I love most about each of these methods is that each can apply to different types of learner. Some are more hands on, some are more visual and others are more mental. As I am going into teaching, I can implement each of these methods into my classroom so that each of my students is able to learn this foundational mathematical concept in their own learning style.

References

[1] A. Bogomolny, Peasant Multiplication from Interactive Mathematics Miscellany and Puzzles
http://www.cut-the-knot.org/Curriculum/Algebra/PeasantMultiplication.shtml, Accessed 30 January 2015

[2] Lattice multiplication. (n.d.). Retrieved January 30, 2015, from http://en.wikipedia.org/wiki/Lattice_multiplication

[3] West, L. (2011). An Introduction to Various Multiplication Strategies. 2-3. Retrieved January 30, 2015, from http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf

[4] Su, Francis E., et al. “Visual Multiplication with Lines.” Math Fun Facts. <http://www.math.hmc.edu/funfacts&gt;.

[5] What is the origin of “how the Japanese multiply” / line multiplication? (2014, July 24). Retrieved January 31, 2015, from http://math.stackexchange.com/questions/877120/what-is-the-origin-of-how-the-japanese-multiply-line-multiplication

[6] Vennebush, G. (2011, May 28). Finger Multiplication. Retrieved January 31, 2015, from https://mathjokes4mathyfolks.wordpress.com/2011/05/28/finger-multiplication/

A New World of Thought in Fractions

I never thought about math as a fluid subject that would be approached differently depending on the needs of a culture.  We are taught from a young age how to do math and what it applies to, but I never thought that in different cultures, in a different time, people’s application of math could be so different from ours.

Let me explore my thought this way.  When I think of a math problem I need to solve on a daily basis, it is usually based around money, or computer memory.  I have five dollars and I want to buy a sandwich and fries.  Do I have enough money?  Or I have 3 GB of data for my phone.  Can I watch my favorite TV show on 4G or do I need to wait until I get home?  Many of the math problems we run into on a day-to-day basis support a monetary society where I have money, so I use that money to get more things.

This is starkly different from what we learned of different cultures in class.  The culture in particular I think of is Egyptian culture.  From the book, Count Like an Egyptian: A Hands-on Introduction to Ancient Mathematics, I learned that in ancient Egypt they had a very different fractional system than we do.  When we think of fractions we have a denominator and a numerator.  I like to think of the denominator as a bucket with n places for an object. The numerator is how many objects we have in the bucket, or how full it is.  In Egypt they had a very different system.  They represent fractions as a single number with a line over it.  The number represented an amount and the line indicated that it was a fraction.  It is a little foreign to us, but if the Egyptians wrote 6, with a line over the six, then we could think of it as 1/6.  It is important to note, and I will discuss later that this system can represent any fraction.  It would just take a bit more work in order to do that.

Why did they do it that way and why do we do things the way we do?  I think in our society our number system fulfills our desire to fill and make sure we have enough.  Our fractional system is very supportive of the money we use, because money is how we support ourselves. To elaborate on this I will use my bucket analogy for fractions. If you recall I said the denominator in our fractional system is like a bucket with room for n amount of objects.  The numerator tells us how many objects are in the bucket.  If the numerator and denominator are the same then we have filled one bucket. We use this all the time when we go shopping food.  When we shop the denominator is the price of what we want to buy.  The numerator is how much money we have.  If we have enough money, which represents the numerator, to fill the price, which represents the denominator, then we can get that item.  Or using my analogy you could say we filled the bucket.

In ancient Egypt their fraction system also could have supported their means of commerce.  They could have had more of a barter system were you worked for food and your master or boss gave you a portion of what you helped him produce.  For example if ten workers made 12 loaves of bread the boss possibly would have taken four for himself, leaving eight for the workers.  Using the Egyptian fractional system he could quickly and efficiently think, I have eight loaves for ten workers.  I will divide 5 loaves into halves giving me 2, with a line over the 2(1/2), which is, half a loaf for each worker.  Now I still have 3 loaves left.  If I divide those into fourths or 4, with a line over the 4(1/4), then I will have given each worker ½ a loaf and ¼ a loaf and there will be ½ a loaf left.  Know all I need to do is break that into tenths, but since it was a half loaf that would actually be twentieths.  That gives me 2 4 20, all with a with a line over them, which to us would be ½+1/4+1/20.  Now the boss had divided his loaves evenly and easily.

Learning this got me wondering.  How was it that other cultures did math?  Could I find another unique way fractions were used?  In the article, History of Fractions, Liz Pumfry talks about a Babylonian method of writing fractions.  Their method was also very simple and a little confusing.  To explain the Babylonian fraction system I first have to explain that the Ancient Babylonian number system was base 60.  The Babylonians wrote their fractions as demonstrated in the image below.

Image from nrich.maths.org.

The first grouping of symbols is for twelve and the second is for fifteen.  In Babylonian fractions this would come out to be 12 + (15/60).  That is, if this was a fraction.  Because the ancient Babylonians did not have a symbol for zero or a decimal point this grouping of numbers could have other meanings.

x60	Units	Sixtieths	Number
	12	15	12+15/60=12
12	15		720+15

But why did the Babylonians use this method for fractions?  It seems to me that this method kept their number system simple, but in my quick analysis of this study I have found Babylonian fractions to be limited. In the article Babylonian Mathematics, it says, “Irregular fractions such as 1/7, 1/ 11, etc were not normally not used. There are some tablets that remark, ‘7 does not divide’, or ‘11 does not divide’, etc.” From this it seems we can deduce that the Babylonians disregarded some fractions.  It seems to me this could have limited them in some regards. For example, if they only used sixty as a denominator then the smallest number they could represent would be 1/60.  Let’s say they could increase this, though, using 60² or 60ⁿ.  If this is the case they could represent much smaller numbers, but it would still be difficult to represent values such as 1/7 or 1/13.  They might be able to do this by adding different values together, but that sounds very difficult and sloppy.   From this I conclude that they would lose accuracy with their fractional system.

Despite losing accuracy, addition and subtraction of fractions would be made much easier if the denominator was always sixty or a power of sixty.  This would make it easier for them to teach fractions as well as learn fractions.  They would not have to worry so much about finding a common denominator as we do.

It is very interesting to note that the Babylonian representation of fractions is very similar to our representation of decimals.  It is, in fact, so similar that I feel it is important to point out.  Our decimal system is base 10.  If we write 0.1 we are essentially writing 1/10.  This is essentially the exact same as the Babylonian system except they are using base sixty.  This is in fact so similar that it causes us to have the same problem representing some fractions.  If you want to write 1/7 in our decimal system you will quickly realize that this is impossible.  There is no concrete way to represent 1/7 in a base ten system.

It is very interesting to think about these different methods for representing fractions.  The Egyptians, if you think about it, actually had a very strong system that, while confusing, could represent all fractions very accurately.  It also suited their needs very well.  The Babylonians had a system very similar to our decimal system.  It seems foreign to us to use base sixty, but base ten is all we know and if they were confronted with our decimal system they would probably find it similarly confusing.  Our fractional system is, I believe, very strong, but in some ways I look at the Egyptian method and think it could have been very helpful when I wanted to share candy with friends or at the dinner table when everyone is fighting to make sure they get their equal portion of food.

In my studies I could not find any other Ancient Babylonian use of fractions.  I am also left to speculate on their reasons for their fractional system.  It is interesting to consider what a different cultures mathematical systems might have been and speculate as to why they used the method they did.

Sources

http://nrich.maths.org/2515

Count Like an Egyptian: A hand-on Introduction to Ancient Mathematics by David Reimer

http://www.math.tamu.edu/~dallen/masters/egypt_babylon/babylon.pdf

Egyptian Fractions: From Mythology to Computation

Horus and Set. Image: Soutekh67, via Wikimedia Commons.

While we in the United States often associate the All Seeing Eye with the Illuminati or the little eye on top of the pyramid on the dollar bill, in Egypt it is better known as the Eye of Horus – a symbol of healing, life, and resurrection. In Egyptian mythology, Horus was the son of Isis and Osiris, king of Egypt. Osiris had a brother named Set, who after years of watching his brother bring prosperity and joy to the people of Egypt became jealous of his brother and killed him to claim his throne. Once he had come of age, Horus sought to reclaim the throne that was rightfully his. In a battle between Horus and Set, Set gouged out Horus’s eye and ripped it into six pieces (the fight wasn’t too one sided – Set lost a testicle). Seeing the damage of the rightful heir to Egypt, the god Thoth collected the pieces of Horus’s eye and restored them using magic. Thus, the Eye of Horus represents health or wholeness.

The Egyptians ascribed a specific set of unit fractions to the six parts of the Eye of Horus. Each fraction is associated with one of the pieces that the eye was ripped into as well as each of the five senses (sight, smell, taste, hearing, touch) plus a sixth sense represented by the Egyptians as thought. These fractions, 1/2 for smell, 1/4 for sight, 1/8 for thought, 1/16 for hearing, 1/32 for taste, and 1/64 for touch, were often used to measure amounts of pigment, ingredients for medicines, and grain.

It is interesting to note that the Horus Eye fractions were the only unit fractions used in dividing grain and that they were written differently from other unit fractions when used in this context. The base unit of grain used by the Egyptians was the hekat which is approximately 1/8 of a modern day bushel. Rather than using standard unit fraction notation for hekat, each piece of the Horus Eye hieroglyphic became a symbol for each fraction (see table below). That way, if the symbol for a specific part of the Horus Eye was used, it was known to measure a fraction of hekat.

The only exception to this was ro. If the fraction required was less than 1/64, then a seventh unit fraction, ro, was used. Like the Horus Eye fractions, ro was not written as a typical unit fraction, but was symbolized by an open mouth hieroglyphic. One ro was somewhere between a teaspoon and a tablespoon and was used to measure 1/320 hekat. I was not able to find any writings about the origin of ro or why 1/320 might be a significant unit fraction other than 5 ro = 1/64 hekat.

Fractional representation of the Eye of Horus. Image: landofpyramids.org.

From today’s perspective, this collection of numbers makes up the first six terms of a geometric series whose sum converges to one. It is interesting that the symbol for “whole” would only sum to 63/64 in Egyptian times. Some scholars think that the missing 1/64 represents the magic used to reassemble the eye to make it whole. Some consider it intentionally imperfect because mortals cannot achieve the perfection of the gods. Still others think it has value in relation to the Egyptian unit fraction ro. Whatever the reason may be, this collection of sacred unit fractions of the form 1/2ⁿ is just one of many forms of Egyptian mathematics that is derived from the fraction 1/2.

As a matter of fact, most of Egyptian mathematics is centered around halving or doubling quantities and manipulating those halved or doubled quantities to perform calculations. The only additional multiplier often seen in Egyptian mathematics is 2/3, but even this appears to be a result of manipulations of 1/2 (discussed below). The fraction 3/4 is also seen on rare occasion, but I couldn’t find any records or calculations based on this.

Archaeologists have found many Egyptian artifacts containing mathematical tables that were most likely used as reference materials by scribes during computation. Many examples of such tables can be found in the Rhind Mathematical Papyrus (RMP). The Recto of the RMP contains a table of unit fraction sums where the sum is equal to 2/n and n is an odd numbers between 3 and 101. Another table in the RMP lists the results of finding 2/3 of unit fractions with odd denominators. Problem 61 of the RMP begins with a table of five unit fractions and the results of halving those unit fractions. Elsewhere in the RMP, there is a table of doubled odd unit fractions. The lack of tables to describe operations with fractions other than 1/2 and 2/3 further supports the hypothesis that Egyptians strictly used these fractions to obtain results for other fractional quantities. Also, the lack of scratch work or steps along with the ordering of the problems suggests that these were reference tables rather than independent problems. This is particularly clear in Problem 61 of the RMP because the table is given before calculations were made in the first and second parts of the problem that clearly used the values in the table in their computations.

The Egyptians appear to have developed various algorithms for solving specific types of problems. For example, Problems 32 and 34 of the RMP show two sets of equations that exhibit the characteristic, if a*x=b, then (1/b)*x=(1/a). No additional work is provided around the problems, indicating that either scratch work was done elsewhere or this was a general rule known to Egyptian scribes.

In calculating halves of unit fractions described as a sum of other unit fractions, the Egyptians knew to double the denominator of each unit fraction in the sum. An example of this is found in problem 1 the Egyptian Mathematical Leather Roll (EMLR). In this problem, 1/4 is equated to 1/7+1/14+1/28. By doubling, the result is 1/8 is equal to 1/14+1/28+1/56.

A similar process is used to calculate 1/3 of a known unit fraction sum. Interestingly, Egyptians did not simply multiply their denominators through by three, likely because they were so dependent on their tables of halves and two-thirds. Instead multiple problems in the RMP show that scribes would first calculate 2/3 of each unit fraction and then calculate 1/2 of each of the resultant fractions to get to 1/3 of each of the original unit fractions in the sum.

The use of 2/3 instead of 1/3 is generally thought to be a result of manipulations of 1/2. There are many problems in the RMP that show the process of finding 2/3 of any unit fraction as a sum of other unit fractions. Problem 61B of the RMP show the Egyptians understood that 2/3 of any unit fraction, 1/n can be written as (1/2n)+(1/6n). For the case of even unit fractions, this is always appears to be simplified to 1/(n+(n/2)). Both of these calculations simply rely on manipulating halves or wholes of the original fraction to calculate the desired fraction.

Another interesting relation known the Egyptian scribes is demonstrated by ten, mostly successive lines in the EMLR. In Mathematics in the Time of the Pharaohs, Richard J. Gillings calls this the G Rule: “If one unit fraction is double another then their sum is a different unit fraction if and only if the larger denominator is divisible by 3. The quotient of the division is the unit fraction of the sum.” Many examples of this rule are written with no scratch work or intermediate steps shown such as line 11 where 1/9+1/18=1/6. But amongst those problems are problems of a slightly different form. Lines 1, 2, and 3 of the EMLR show that 1/10+1/40=1/8, 1/5+1/20=1/4, and 1/4+1/12=1/3 respectively. These seem to follow the same principal of the G Rule, but for cases when one fraction is triple or quadruple another and the larger fraction is divisible by four or five respectively. According the Gillings, this suggests that the Egyptians had a more inductive understanding of the G Rule: “If one of two unit fractions is K times the other, then their sum is found by dividing (K-1) into the larger number, providing the answer is an integer.”

From all these translations and analyses of original sources, I found it interesting that the groupings of problems on different papyri suggest mathematical rules that Egyptian scribes were familiar with but are not explicitly proven. This suggests to me that the Egyptians discovered rules of mathematics by discovering patterns through repeated computation and if those patterns were regularly helpful in further computations they were organized and made into reference tables. It was strange to me that many of these similar problems are not listed in any particular order or group all together unless they appear in a designated table. To me, this would suggest that these problems were done for practice, but so little information is known about the origins of these sources that it is difficult for even experts to deduce their original purpose.

 

Sources:

http://www.laits.utexas.edu/cairo/teachers/osiris.pdf

http://www.egyptianmyths.net/mythisis.htm

http://www.landofpyramids.org/eye-of-horus.htm

http://www.ancientegyptonline.co.uk

http://www.britishmuseum.org

Gillings, Richard J. Mathematics in the Time of the Pharaohs. Cambridge, Mass. MIT, 1972. Print

Golden Ratio: the fingerprints of God

The Golden Ratio is an interesting topic that pops up in many parts of our lives. Personally, I was told about this for the first time by advertisements of cosmetic and beauty product industries. As a promotion strategy, they commercially (ab)use this concept to entice many girls to aspire to seemingly dazzling idea of achieving “golden” and “perfect ratio.” The name itself demonstrates enough to give an impression of perfect beauty.

The Golden Ratio had been discovered and rediscovered over time historically, which is why it goes under many names: golden mean, golden proportion, divine proportion, etc. The earliest appearance of the Golden Ratio in history is found in design of Great Pyramids in Egypt. In ancient Greece, Euclid discussed it in Book 6, Proposition 30, in his work “Elements” in 300 BC. He showed how to divide a line at the ratio 0.6180399… : 1, which he referred to “dividing a line in the extreme and mean ratio.”

Image courtesy of http://www.goldennumber.net, Gary B. Meisner.

He took a line that is one unit long and divided the line in two parts, such that the ratio of the shorter part of the line to the longer part is the same as the ratio of the longer part to the whole line; that gives a quadratic equation x/(1-x) = (1-x)/1, which yields two solutions x = (1 +/- √5) /2 . Since the ratio between positive quantities has to be a positive number, x= (1 + √5) /2 = 1.618… The term “mean” he used gave rise to the name golden mean, and it is considered the first written reference to the Golden Ratio. After Euclid, many mathematicians extensively studied the Golden Ratio and its unique properties, and since the early 1900s at Mark Barr’s suggestion, they started using the Greek letter phi (Φ) to symbolize the Golden Ratio.

In architecture and arts as well, the Golden Ratio has been a popular topic. The design of Parthenon in Athens, built by the ancient Greeks from 447 to 438 BC, appears to have features of the Golden Ratio. The scholars speculate that Phidias, a Greek sculptor and mathematician, designed the Parthenon based on his studies of Phi. The Golden Ratio can be found on the grid lines and the root support beam. Also the ratio of the structural beam on top of the columns to the height of the columns, and distance ratio of the width of the columns to the center line of the columns exhibits the ratio of 0.618… : 1. Some people question this speculation of the Golden Ratio being applied in the famous structure because first, there is no concrete evidence or written documentation that Phidias was aware of the Golden Ratio when designing the Parthenon, and second, time and history have damaged its original features and dimension, leaving scholars with no choice but to conjecture based on the remaining structure. Thus, it may not be accurate to conclude that Greeks have applied the Golden Ratio in the construction of the Parthenon.

During the period of Renaissance, Leonardo Da Vinci was known to have applied the Golden Ratio in his art works, which was called sectio aurea, meaning “golden section” in Latin. His illustrations of polyhedra in De Divina Proportione, “On the Divine Proportion,” by Luca Pacioli in 1509 and his other works including the Last Supper and Mona Lisa indicates that he incorporated the Golden Ratio to define the fundamental proportions of his drawings. Other Renaissance artists also used the Golden Ratio extensively in their paintings and sculptures to achieve balance and beauty, and it was also called as divine proportion after Da Vinci’s work in Pacioli’s book.

Image: Polyhedron drawn by Da Vinci, via Wikimedia Commons.

But the most interesting thing about the Golden Ratio, in my opinion, is found in mathematics. Mathematics sees the Golden Ratio as unique rather than beautiful. It has several properties that make it unique among all numbers.

1. If you square Phi, you get a number exactly 1 greater than itself.

Φ^2  = Φ + 1= 2.618…

2. If you take the reciprocal of Phi, you get a number exactly 1 less than itself. The reciprocal of Phi is often written as phi with lowercase p.

1/Φ  = Φ – 1= 0.618…

3. Using two properties above, Phi can be expressed in nested radicals and continued fractions.

As in #2, Φ = 1+ 1/Φ.  This can be expanded recursively. Given the initial approximation Φ(0)=1, in order to get the next approximation in the sequence Φ(n+1), we just add 1 to the reciprocal of the previous approximation Φ(n). This gives a formula Φ(n+1) = 1+ 1/Φ(n). Now we substitute the successive values of Φ(n) in the formula repeatedly to build up a sequence of continued fractions. The limit of these continued fractions as n goes to infinity is phi.

For nested radicals expression, take a look at the property in #1. The equation Φ^2  = 1 + Φ likewise produces the continued square root.

Image courtesy of http://www.goldennumber.net, Gary B. Meisner.

Other than these amazing properties, Phi is connected to other mathematics. Most notable link is Fibonacci sequence, discovered by Leonardo Fibonacci, an Italian mathematician, in 1175 AD, but it is a mystery if Fibonacci was aware of the link between what he had discovered and Phi.

The Fibonacci sequence is defined recursively. It starts off with two ones, and each successive term is the sum of the two terms before it. So the Fibonacci numbers are 1, 1, 2, 3, 5, 8, 13, 21, 34,… Johannes Kepler who showed that the Golden Ratio is the limit of the ratios of successive terms of the Fibonacci sequence. If we take the ratio of two successive numbers and continue on the fractions, we can see that ratios are getting very close to Phi.

2/1 = 2

3/2 = 1.5

5/3 = 1.666666…

8/5 = 1.6

13/8 = 1.625

…

233/144 = 1.618055556…

377/233 = 1.618025751…

The fractions of Fibonacci numbers give values that are alternatively higher and lower than Phi, and converge on Phi as the number increases. So the limit of F(n+1)/F(n) when n is approaching to infinity is equal to Phi.

Image: Wikimedia Commons.

It is not only mathematics that connects Phi and Fibonacci. The spiraling growth of leaves, flower petals, and seed pods follows Phi rotation. This minimizes the amount of overlap of any leaf by those leaves located higher on the stem, which allows each leaf to receive the maximum amount of sunlight for photosynthesis. So it is not a coincidence that Fibonacci numbers are commonly found in the plant’s spiral growth pattern of new cells because they essentially express the Phi ratio. Although it is not absolutely true for all plant species, both Phi and Fibonacci explain intricate and sophisticated patterns found in nature. Phi is amazingly connected to every parts of the world, which explains why its reference is so ubiquitous in a variety of areas such as arts, architectures, and mathematics. It has played a significant role in deeper understanding of life and universe, and I think it is why people often call it “the fingerprint of God.”

sources

https://archive.org/details/euclid_heath_2nd_ed

Mathematics of Phi, 1.618, the Golden Number

http://mathworld.wolfram.com/GoldenRatio.html

http://jwilson.coe.uga.edu/emt669/student.folders/frietag.mark/homepage/goldenratio/goldenratio.html

http://nrich.maths.org/2737

Egyptian Numbers: Counting By Ten

When most people think of early mathematics, the first thing that comes to mind is probably Archimedes or Pythagoras of ancient Greece; or perhaps ancient Mesopotamia and its thousands of clay tablets, many of them containing math problems.  Few people think of ancient Egypt. This is mainly due to the fact that little is known about ancient Egyptian math in comparison to these other civilizations. However, by looking at what we do know about Egyptian math and the feats of engineering they accomplished with it, we can recognize how complex and sophisticated it was.

A fragment from the Rhind Mathematical Papyrus. Image: Public domain, via Wikimedia Commons.

The majority of our knowledge of ancient Egyptian math comes from two papyri: the Rhind Mathematical Papyrus, which was originally written about 1985-1975 BCE; and the Moscow Mathematical papyrus, dating from around 1850 BCE. Math problems were not written on the walls of temples or great monuments in Egypt, so all math was probably done on papyrus or other perishable media, meaning that many mathematical works have not come down to us. This in in contrast to the mathematical documents from Mesopotamia, which were primarily done on clay tablets that are not as susceptible to the elements and ravages of time.

The ancient Egyptians probably developed the first base ten numerical system in human history. It was fully in use around 2700 BCE and perhaps even earlier. They had different symbols representing the powers of ten. A straight vertical line represented one, 10 was shown by a drawing of a hobble for cattle, a picture of a coil of rope served as a symbol for 100, a lotus plant delineated 1,000, a bent finger for 10,000, a tadpole or a frog for 100,000 and the picture of a god, perhaps Heh, represented 1 million. Although the Egyptian numerals were in a decimal system, it was not a positional place value system like the decimal system we use, or the sexagesimal (base 60) system developed by the Mesopotamians. Multiples of the powers of ten were written by repeating the symbol as many times as needed, and although they had a symbol for 1 million, other large numbers would have been very tedious to write. For instance, the number 987,654 would have required 39 characters. This Egyptian system possibly had an influence on the later Greek numerical system, but the Greeks improved upon it, creating a different symbol for each number 1-9, and other symbols for 20, 30 and so on.

Parts of the Eye of Horus were used to write fractions. Image: BenduKiwi, via Wikimedia Commons.

The Egyptians also had notation for fractions, although all Egyptian fractions were unit fractions (meaning they always had one in the numerator), with only two exceptions, 2/3 and 3/4. Fractions were marked by the hieroglyph for ‘R’ which is a long skinny oval, very similar in shape to the Eye of Horus. In fact, in an ancient Egyptian myth, the evil god Seth attacked his brother the god Horus and in the fight Seth gouged out the eye of Horus and tore it into pieces, fortunately the god Throth was able to put Horus’s eye back together and heal it. Thus, to honor the gods and this myth, whenever the Egyptians used fractions in relation to their measurement of volume, which is the hekat, the commonly used fractional parts were transcribed by using the corresponding parts of the Eye of Horus.

The great feats of engineering that the ancient Egyptians accomplished would have required an enormous amount of sophisticated math. The pyramids, for instance, are considered a marvel of mathematics and engineering. The base of the pyramids are almost perfect squares which the Egyptians would have achieved by using trigonometry, like the 3-4-5 trick. It was known in Egypt that a triangle with 3, 4 and 5 unit sides would always be a perfect right triangle. This Pythagorean triple, observed by the Egyptians long before Pythagoras, is sometimes called an “Egyptian triangle.” The Egyptians would have utilized this rule of geometry when laying out the base of a pyramid by tying knots in rope at 3, 4 and 5 unit intervals. Other tricks of trigonometry were known as well. The Rhind Mathematical Papyrus contains an equation for calculating the slope of a pyramid’s face, which is the same thing as finding the cotangent. It is also likely that they knew how to find a pyramid’s volume.

It is unfortunate that more is not known about the mathematics that were used by the ancient Egyptians, because they were obviously very skillful and innovative, and they must have been among the first people to develop important mathematical principals.

Sources:

http://discoveringegypt.com/egyptian-hieroglyphic-writing/egyptian-mathematics-numbers-hieroglyphs/

Click to access egypt.pdf

http://www.britishmuseum.org/explore/highlights/highlight_objects/aes/r/rhind_mathematical_papyrus.aspx

http://www.touregypt.net/featurestories/numbers.htm

Base 1 and ancient Egyptian math

Different ways of writing 8 in unary. Image: Wapcaplet, via Wikimedia Commons.

Earlier in class, we started to discuss different bases for mathematical systems.  I brought up base 1 and we all got into a debate as to whether or not base 1 actually makes sense.

The answer is, it depends on who you ask.  To understand why, we need to really know what it means for a number to be represented in base “n”.  A way of rigorously defining this is to define a sequence of whole numbers a₀, a₁, a₂,…, with each a being less than n, such that the number you want to represent is equal to a₀+a₁*n+a₂*n²+…  For example, representing 5 in base 2 would give us a₀=1, a₁=0 and a₂=1, because 1 + 0*2 + 1*4 = 5.  Then, it is a simple matter of writing the number as a₀a₁a₂…, or in this specific case, 101.

We want to have 4 properties when doing this:

1.  Each number has at least 1 representation.

2.  Each number has no more than 1 representation.

3.  Each representation corresponds to at least one n.

4.  Each representation corresponds to no more than 1 n.

Some of these properties are more important than others.  As it turns out, properties 1 and 4 are key.  Property 1 guarantees that anything we want to write in our base, we can.  It’d be silly if we had a numerical system that couldn’t list numbers over 1,000,000, for example.  Property 4 is even more important:  it guarantees that no two different numbers can look the same.  It would be really silly if we looked at a number and had to guess whether or not it was 3 or 4.

As it turns out, to have ALL of these properties, we must specify that n is greater than or equal to 2.  Why?  If we set n equal to 1, then the restriction that each a must be less than n requires ALL a’s to be equal to 0.  Meaning that 0 becomes the ONLY number we can represent.  Not very useful.

Well, let’s see if we can salvage this.  Let’s say we drop the restriction that each of the a’s has to be less than our n.  Now our situation becomes more hopeless.  In base 1, we could, for example, write 6 as 51, or 2211, or 312, or 501, and so on.  While it may be clear what each of these numbers is, there’d be no point in being able to write it so many ways.  And if we picked the simplest one to represent our system, why not just pick the number itself?  And if we’re representing a number by simply itself, why complicate things and work in this odd base-1 system anyways?

This is why when mathematicians and computer scientists talk about base-1, they are mostly referring to the unary mathematical system.

If you want to represent a number in the unary system, say N, all you do is repeat the same symbol N times.  So 10 becomes ||||||||||, and so on.  This type of numerical representation is a lot like counting on your fingers or tallying a certain number of objects.  It’s also useful for birthday cakes.

Now, let’s see if this satisfies the above 4 conditions:

1.  Each number has at least 1 representation.  Clearly true

2.  Each number has no more than 1 representation.  True

3.  Each representation corresponds to a number.  If a representation has N slashes, the number it represents is simply N.  True

4.  Each representation corresponds to no more than one number.  If a number represents N, it can’t represent anything else in this system.  True.

Alright, it looks like we have a good system.  Now, let’s take a look at how one would add, subtract, multiply or divide.  Addition and subtraction are quire easy in the unary system:  For addition, just combine the two sets of slashes, and for subtraction take away a certain number of slashes from one of them.  In fact, division and multiplication are also quite easy.  Calculating N/M is as easy as crossing out M slashes from the number N, marking that as a 1, and repeating until you no longer have M slashes left.  N*M is as simple as writing down N slashes M times.

The advantages of the unary system is that you do not need to memorize any multiplication tables to do multiplication.  As long as you know the system, it’s incredibly simple.  The obvious downside is that even for relatively small numbers multiplied by one another the result can become extremely large extremely quickly.  You can think of it sort of as a trade-off:  In base 10, for example, multiplication and division are much more difficult, but can be much, much quicker to calculate and much easier to understand.

How this actually relates to math history is through ancient Egyptian mathematics.  What’s interesting about their style of mathematics is that it incorporates elements of both the unary system and the base 10 system, and isn’t truly one or the other, but a hybrid of both.  In the ancient Egyptian system, a 1 is represented as |, 2 as ||, and so on.  But 10 gets its own symbol, represented as an upside down U, and 100, 1,000, 10,000, 100,000 and 1,000,000 all have their own representation.  This is somewhat “in-between” the two bases:  on the one hand, the order in which you place the digits doesn’t matter, but on the other, numbers become quite a bit longer than they need to be.

This goes to show one of the cooler parts of mathematics:  when you take an idea such as “dividing by 0” or “base-1” to its logical extreme, you start to understand deeper relationships between numbers, and can come up with some very interesting results.

Sources used:

http://en.wikipedia.org/wiki/Unary_numeral_system

http://math.stackexchange.com/questions/371972/what-would-base-1-be