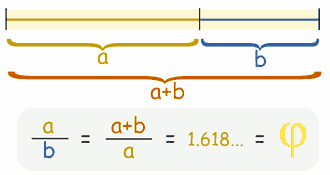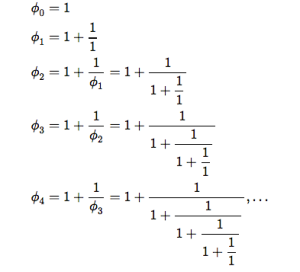Leonardo of Pisa – The Great Fibonacci

Figure 1-Fibonacci. Image: Public domain, via Wikimedia Commons.

Most mathematically inclined people are familiar with the famous and unique Fibonacci sequence. Defined by the recurrence relation (*) F_n=F_n-1+F_n-2 with initial values F₁=1 and F₂=1 and (or sometimes F₀=1 and F₁=1), the Fibonacci sequence is an integer sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …) with many remarkable mathematical and real world applications. However, it seems that few are as well informed on the man behind this sequence as they are on the sequence itself. Did you know that Fibonacci didn’t even discover the sequence? Of course not! Predating Fibonacci by almost a century, the so called “Fibonacci sequence” was actually the brainchild of Indian mathematicians interested in poetic forms and meter who, through studying the unique arithmetic properties of certain linguistic sequences and syllable counts, derived a great deal of insight into some of the most fascinating mathematical patterns known today. But with a little bit of time (few hundred years), some historical distortion, inaccurate accreditation[1], and a healthy dose of blind western ethnocentrism and voila! Every high school kid in America now thinks there is a connection between Fibonacci and pizza. Or is it Pisa? (That’s a pun, laugh.) While often given more credit than deserved for the “discovery” of the sequence, Fibonacci was nonetheless an instrumental player in the development of arithmetic sequences, the spread of emerging new ideas, and in the advancement of mathematics as a whole. We thus postpone discussion of Fibonacci’s sequence – don’t worry, we shall return – to examine some of the other significant and often overlooked contributions of the “greatest European mathematician of the middle ages.”^[1]

Born around the year 1175 in Pisa, Italy, Leonardo of Pisa (more commonly known as Fibonacci) would have been 840 years old this year! (Can you guess the two indexing numbers between which Fibonacci’s age falls?[2]) The son of a customs officer, Fibonacci was raised in a North African education system under the influence of the Moors.[3] Fibonacci’s fortunate upbringing and educational experience allowed him the opportunity to visit many different places along the Mediterranean coast. It is during these travels that historians believe Fibonacci may have first developed an interest in mathematics and at some point come into contact with alternative arithmetic systems. Among these was the Hindu-Arabic number system – the positional number system most commonly used in mathematics today. It appears that we owe a great deal of respect to Fibonacci for, prior to introducing the Hindu-Arabic system to Europe, the predominant number system relied on the far more cumbersome use of roman numerals. It is interesting to note that while the Hindu-Arabic system may have been introduced to Europe as early as the 10^th century in the book Codex Vigilanus, it was Fibonacci who, in conjunction with the invention of printing in 1482, helped to gain support for the new system. In his book Liber abbaci[4], Fibonacci explains how arithmetic operations (i.e., addition, subtraction, multiplication, and division) are to be carried out and the advantages that come with the adoption of such a system.

Figure 2-Golden spiral. Image: Weisstein, Eric W. “Golden Spiral.” From MathWorld–A Wolfram Web Resource.

Whereas the number system most familiar to us uses the relative position of numbers next to each other to represent variable quantities (i.e., the 1’s, 10’s, 100’s, 1000’s, … place), Roman numerals rely on a set of standard measurement symbols which, in combination with others, can be used to express any desired quantity. The obvious problem with this approach is that it severely limits the numbers that can be reasonably represented by the given set of symbols. For example, the concise representation of the number four hundred seventy eight in the Hindu-Arabic system is simply 478 in which “4” is in the hundreds place, “7” is in the tens place, and “8” is in the ones place. In the Roman numeral system, however, this same number takes on the form CDLXXVIII. As numbers increase arbitrarily so does the complexity of their Roman numeral representation. The adoption of the Hindu-Arabic number system was, in large part, the result of Fibonacci’s publications and public support for this new way of thinking. Can you imagine trying to do modern mathematical analysis with numbers as clunky as MMMDCCXXXVIII??? Me either. Thanks, Fibonacci!

Fibonacci’s other works include publications on surveying techniques, area and volume measurement, Diophantine equations, commercial bookkeeping, and various contributions to geometry.^[4] But among these works nothing stands out more than that of Fibonacci’s sequence – yes, we have returned! Among the more interesting mathematical properties of Fibonacci’s sequence is undoubtedly its connection to the golden ratio (shall be defined shortly). To illustrate, we look momentarily at the ratios of several successive Fibonacci numbers. Beginning with F₁=1 and F₂=1 we see that the ratio F₂/F₁=1. Continuing in this manner using the recurrence relation (*) from above or any suitable Fibonacci table we find that F₃/F₂=2, F₄/F₃=3/2, F₅/F₄=5/3,F₆/F₅=8/5, F₇/F₆=13/8, F₈/F₇=21/13, … As the indexing number tends to infinity, the ratio of successive terms converge to the value 1.6180339887… (the golden ratio) denoted by the Greek letter phi. We may thus concisely represent this convergent value by the expression as the lim n–> infinity (F_n+1/F_n). Studied extensively, the golden ratio is a special value appearing in many areas of mathematics and in everyday life. Intimately connected to the concept of proportion, the golden ratio (sometimes called the golden proportion) is often viewed as the optimal aesthetic proportion of measurable quantities making it an important feature in fields including architecture, finance, geometry, and music. Perhaps surprisingly, the golden ratio has even been documented in nature with pine cones, shells, trees, ferns, crystal structures, and more all appearing to have physical properties related to the value of (e.g., the arrangement of branches around the stems of certain plants seem to follow the Fibonacci pattern). While an interesting number no doubt, we must not forget that mathematics is the business of patterns and all too often we draw conclusions and make big picture claims that are less supported by evidence and facts than we may believe. There is, in fact, a lot of “woo” behind the golden ratio and the informed reader is encouraged to be weary of unsubstantiated claims and grandiose connections to the universe. It is also worth mentioning that, using relatively basic linear algebra techniques, it is possible to derive a closed-form solution of the n-th Fibonacci number.

Figure 3-Computing the 18th Fibonacci Number in Mathematica.

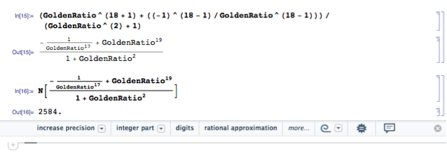
Omitting the details (see link for thorough derivation), the n-th Fibonacci number may be computed directly using the formula F_n=((φ)⁽ⁿ⁺¹⁾+((-1)^(n-1)/(φ)^^(n-1))/((φ²)+1).^[5] While initially clunky in appearance, this formula is incredibly useful in determining any desired Fibonacci number as a function of the indexing value n. For example, the 18-th Fibonacci number may be calculated using F₁₈=((φ)⁽¹⁸⁺¹⁾+((-1)^(18-1)/(φ)^^(18-1))/((φ²)+1)=2584. Comparing this value to a list of Fibonacci numbers and to a Mathematica calculation (see picture above), we see that the 18-th Fibonacci number is, indeed, 2584. Without having to determine all previous numbers in the sequence, the above formula allows us to calculate directly any desired value in the sequence saving substantial amounts of time and processing power.

From the study of syllables and poetic forms in 12^th-century India to a closed-form solution for the n-th Fibonacci number via modern linear algebra techniques, our understanding of sequences and the important mathematical properties they possess is continuing to grow. Future study may reveal even greater mathematical truths whose applications we cannot yet conceive. It is thus the beauty of mathematics and the excitement of discovery that push us onward, compel us to dig deeper, and to learn more from the world we inhabit. Who knows, you might even be the next Leonardo of Pizza – errrrr Pisa. What patterns will you find?
[1] French mathematician Edouard Lucas (1842-1891) was the first to attribute Fibonacci’s name to the sequence. After which point little is ever mentioned of the Indian mathematicians who laid the groundwork for Fibonacci’s research.

[2] Answer: n=15 –> 610 and n=16 –> 987.

[3] Medieval Muslim inhabitants of the Maghreb, Iberian Peninsula, Sicily, and Malta.^[2]

[4] Translation: Book of Calculation^[3]

Bibliography

 ^[1] Knott, Ron. Who Was Fibonacci? N.p., 11 Mar. 1998. Web. 27 Apr. 2015.

^[2] “Moors.” Wikipedia. Wikimedia Foundation, n.d. Web. 27 Apr. 2015.

^[3] Leonardo Pisano – page 3: “Contributions to number theory”. Encyclopædia Britannica Online, 2006. Retrieved 18 September 2006.

^[4] “Famous Mathematicians.” The Greatest Mathematicians of All Time. N.p., n.d. Web. 28 Apr. 2015.

 ^[5] Grinfeld, Pavel. “Linear Algebra 18e: The Eigenvalue Decomposition and Fibonacci Numbers.” YouTube. YouTube, 2 Dec. 2014. Web. 28 Apr. 2015.

 Figure 1: Fibonacci. Digital image. Wikimedia Foundation, n.d. Web. 27 Apr. 2015.

Figure 2: Golden Spiral. Digital image. Mathworld. Wolfram, n.d. Web. 1 May 2015.

Figure 3: Ross, Andrew Q. Closed-Form Computation of Fibonacci. Digital image. Mathematica, 28 Apr. 2015. Web. 28 Apr. 2015.

Nature and The Golden Ratio

We often hear people ask: “Why do we have to take math? We will never use it again.” The fact of the matter is math is all around, wherever we look. Even when you are camping up in the mountains, you can find something that is related to math. In the mountains, nature has made the golden ratio very prevalent in flowers and pinecones.

What is the golden ratio? On the website Live Science, the author Elaine J. Hom described it as the following: “The Golden ratio is a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part.” What this is saying in an equation is a/b=(a+b)/a= 1.61803398874989…(ect.). This is also referred to the as phi, and it is an irrational number. This is how the ratio would be represented:

An important sequence is introduced when we are talking about the golden ratio. This sequence is called the Fibonacci sequence: 0,1,1,2,3,5,8,13… Each term is the sum in the two previous terms. The more you go to the right of the sequence the ratio of two terms right next to each other it will get closer to the Golden Ratio.

Now you might be asking yourself, “What does this all have to do with nature?” It has everything to do with nature. Let’s look at plants first. Usually, the number of leaves on the plant’s stem is arranged in a spiral pattern permitting the amount of sunlight the leaves need. The way the leaves or petals are arranged the Golden Ratio gives the ideal gap between the leaves or petals and they usually end up being a Fibonacci number. When we look at petals, we notice that they too have Fibonacci arrangements because when looking at them you will see a  pattern. Each of these patterns you will see on petals of a flower all represent the Golden Ratio in their own way.

Looking at the pine cone you will notice the spiral that it naturally takes. Image: Böhringer Friedrich, via Wikimedia Commons.

Just like the petals and the leaves, pinecones are also in a spiral shape. Therefore, they too have Fibonacci qualities. They have two sets of spirals, one going in the clockwise direction and one going in counter clockwise direction, as you can see in the picture to the left. The numbers of spirals in the pinecones are almost always consecutive Fibonacci numbers. For example, there can be 8 spirals clockwise and 5 spirals counter clockwise. This shows the pinecones are related to the rational approximation of the Golden ratio (8/5).

Math is everywhere in our daily life. The Golden Ratio cannot only be seen in nature but it can be seen in everything around us. The Golden Ratio works hand in hand with the Fibonacci sequence.  The more to the right we go in a Fibonacci sequence the more we can relate it back to the Golden Ratio. If we would just take a minute and look around, we will see that math is important and relevant in our daily lives.

For more information about nature, the Golden Ratio and Fibonacci watch this really interesting and quick video  from Vi Hart. https://www.youtube.com/watch?v=lOIP_Z_-0Hs

Sources

• http://www.livescience.com/37704-phi-golden-ratio.html
• http://mathforum.org/dr.math/faq/faq.golden.ratio.html
• http://jwilson.coe.uga.edu/emat6680/parveen/fib_nature.htm

Num83r5

Right next to learning your A B C’s you learn your 1 2 3’s. Both have a similarity in that they are forms of communication, but do not exist. The purpose of numbers was so that things could have meaning and value .

We have big numbers, small numbers, numbers over numbers called fractions. Numbers that are bigger than zero, numbers that are smaller than zero, numbers that go backwards known as negative numbers and ones that go forwards called positives. We can manipulate numbers with other numbers to make bigger or smaller numbers. Some numbers go forwards so impossibly forever that we can’t put a value to them, only a symbol and a name. These numbers can also go forever backwards too, represented with a dash in front of the symbol. There are imaginary numbers and a number to represent nothing.

Numbers can be used to create patterns or code to mean something. Computer language is called binary, which reads only 1’s and 0’s. Numbers can also create patterns themselves. Sequences are a set of numbers, sometimes they have a pattern and other times they do not. An arithmetic sequence is a pattern that increases or decreases steadily. 1, 3, 5, 7, 9… is an arithmetic sequence that is increasing by 2 every time. Geometric sequences have a pattern that increase or decrease by the same value but don’t necessarily increase or decrease steadily. 2, 4, 8, 16, 32… is a geometric sequence that is multiplied by 2 every time.  Arithmetic and Geometric sequences are fairly common and easy to grasp. Other common patterns are square and cube patterns (1, 4, 9, 16, 25… and 1, 8, 27, 64, 125…), which are just patterns in the numbers. Some patterns incorporate numbers and pictures.

One of the most common number patterns is known as the Fibonacci sequence. Fibonacci’s sequence goes 1, 1, 2, 3, 5, 8, 13, 21… Do you see the pattern? It’s a little trickier than the others but still quite simple. You get Fibonacci’s number by adding the first two numbers to get the next one (1+1=2, 1+2=3, 2+3=5, 3+5=8…). Is there significance in this pattern, or is it just a cool pattern? The answers can found in nature. (http://en.wikipedia.org/wiki/Fibonacci_number)

Start by dividing one number in the fibonacci sequence by the number before it. (3/2=1.5, 5/3=1.66, 8/5=1.6, 13/8=1.625, 21/13=1.615…) Notice how all the numbers start getting closer and closer together towards the same number 1.618? Much like Pi which written shorthand as 3.14, Phi is written shorthanded as 1.618, (although both are irrational and can’t be written out completely in decimal form because they lack an end). Phi is known as the golden number.  The significance of this number is that it is an irrational number. Because of the irrationality of phi, it can’t be written as a fraction which is what makes them vital for plants in nature.

Sunflowers are the easiest to see Fibonacci numbers in. Plants take in light from the sun which means in order to be a good plant and survive, you need to show as much “skin” (leaves/seeds/petals) as you can without overlaps and gaps. The center of sunflowers grow their seeds in a spirally kind of pattern. These seeds rotate from the next at 61.8% (Phi!) of a full rotation, (or about 222.5 degrees). This angle of rotation gives planets the optimal conditions to fit the most seeds in the smallest area possible with the smallest amount of gaps. If one was to take the time to count the seed in a spiral the Fibonacci numbers would appear again, 34 seeds counterclockwise and 55 seeds clockwise. (http://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html) But sunflowers aren’t the only plants to have Fibonacci numbers. Other plants have it; pinecones, pineapples, cauliflower/broccoli tops, are a few examples.

The Fibonacci sequence has both significance and is cool. Some people however have a hard time accepting both facts. Some say nothing has the golden ratio in it, and that it doesn’t exist. Others believe in it so strongly they claim it to be in places it is not. The second group claim the golden ratio/spiral in; nature, nautilus shells, galaxy spirals, hurricane arms, ocean waves, famous paintings (such as the Mona Lisa), The Parthenon, and the ideal human face. These are just a few examples of what they claim to be “golden” items, but not all are. While nature does indeed have the ratio, not everything does, nautilus shells do have aspects of the ratio, but are not how they claim it to be. The case is the same with the Parthenon. Famous paintings such as  Da Vinci’s “Last Supper” and “The Annunciation” do indeed have the golden ratio, but not all paintings do. (http://www.goldennumber.net/golden-ratio-myth/)

As for the ideal human face the myths and the facts are harder to distinguish. The idea isn’t does the human face have the golden ratio in it. The idea is, will an ideal (perfect/attractive) face be made of the ratio. Tons of research has be done to both prove and disprove it, but more evidence suggests that an ideal face will have the golden ratio. Would this suggest that the human mind favors the ratio? Is our mind pre programmed to favor items with the ratio? If so then the mind would favor a form of order in an unorganized (irrational) number. I would think that irrational numbers would make anyone cringe to look at (Or at least I do, and I know I can’t be the only one). There’s no end to them, and they can’t be put into a nice even fraction. That instantly makes them not nice. So why would the mind favor a ratio that is irrational?

In my 9th grade science class we were all required to do a science fair project. I ended up doing mine on soundwaves and when directed at a curve can be heard great distances away despite the volume of the sound. Some friends of mine did theirs on Phi. They wanted to see whether people would favor items in a room that were of the golden ratio versus those that were not. They drew two rooms in a one point perspective, one with Phi the other just slightly off. They would ask people which room they liked more. Next they drew different forms of furniture (couches, tables, chairs, wardrobes) in the same manner. One being Phi the other just a little off, and asked everyone individually which they liked more. What they found was that more people favored the room and items that were the golden ratio over those that were not.

Keep in mind this was an experiment done by high school students in 9th grade, that does not make it an a perfect experiment. But it is an interesting idea to ponder upon.

The digits of Phi written into the symbol of Phi.

 

Golden Ratio: the fingerprints of God

The Golden Ratio is an interesting topic that pops up in many parts of our lives. Personally, I was told about this for the first time by advertisements of cosmetic and beauty product industries. As a promotion strategy, they commercially (ab)use this concept to entice many girls to aspire to seemingly dazzling idea of achieving “golden” and “perfect ratio.” The name itself demonstrates enough to give an impression of perfect beauty.

The Golden Ratio had been discovered and rediscovered over time historically, which is why it goes under many names: golden mean, golden proportion, divine proportion, etc. The earliest appearance of the Golden Ratio in history is found in design of Great Pyramids in Egypt. In ancient Greece, Euclid discussed it in Book 6, Proposition 30, in his work “Elements” in 300 BC. He showed how to divide a line at the ratio 0.6180399… : 1, which he referred to “dividing a line in the extreme and mean ratio.”

Image courtesy of http://www.goldennumber.net, Gary B. Meisner.

He took a line that is one unit long and divided the line in two parts, such that the ratio of the shorter part of the line to the longer part is the same as the ratio of the longer part to the whole line; that gives a quadratic equation x/(1-x) = (1-x)/1, which yields two solutions x = (1 +/- √5) /2 . Since the ratio between positive quantities has to be a positive number, x= (1 + √5) /2 = 1.618… The term “mean” he used gave rise to the name golden mean, and it is considered the first written reference to the Golden Ratio. After Euclid, many mathematicians extensively studied the Golden Ratio and its unique properties, and since the early 1900s at Mark Barr’s suggestion, they started using the Greek letter phi (Φ) to symbolize the Golden Ratio.

In architecture and arts as well, the Golden Ratio has been a popular topic. The design of Parthenon in Athens, built by the ancient Greeks from 447 to 438 BC, appears to have features of the Golden Ratio. The scholars speculate that Phidias, a Greek sculptor and mathematician, designed the Parthenon based on his studies of Phi. The Golden Ratio can be found on the grid lines and the root support beam. Also the ratio of the structural beam on top of the columns to the height of the columns, and distance ratio of the width of the columns to the center line of the columns exhibits the ratio of 0.618… : 1. Some people question this speculation of the Golden Ratio being applied in the famous structure because first, there is no concrete evidence or written documentation that Phidias was aware of the Golden Ratio when designing the Parthenon, and second, time and history have damaged its original features and dimension, leaving scholars with no choice but to conjecture based on the remaining structure. Thus, it may not be accurate to conclude that Greeks have applied the Golden Ratio in the construction of the Parthenon.

During the period of Renaissance, Leonardo Da Vinci was known to have applied the Golden Ratio in his art works, which was called sectio aurea, meaning “golden section” in Latin. His illustrations of polyhedra in De Divina Proportione, “On the Divine Proportion,” by Luca Pacioli in 1509 and his other works including the Last Supper and Mona Lisa indicates that he incorporated the Golden Ratio to define the fundamental proportions of his drawings. Other Renaissance artists also used the Golden Ratio extensively in their paintings and sculptures to achieve balance and beauty, and it was also called as divine proportion after Da Vinci’s work in Pacioli’s book.

Image: Polyhedron drawn by Da Vinci, via Wikimedia Commons.

But the most interesting thing about the Golden Ratio, in my opinion, is found in mathematics. Mathematics sees the Golden Ratio as unique rather than beautiful. It has several properties that make it unique among all numbers.

1. If you square Phi, you get a number exactly 1 greater than itself.

Φ^2  = Φ + 1= 2.618…

2. If you take the reciprocal of Phi, you get a number exactly 1 less than itself. The reciprocal of Phi is often written as phi with lowercase p.

1/Φ  = Φ – 1= 0.618…

3. Using two properties above, Phi can be expressed in nested radicals and continued fractions.

As in #2, Φ = 1+ 1/Φ.  This can be expanded recursively. Given the initial approximation Φ(0)=1, in order to get the next approximation in the sequence Φ(n+1), we just add 1 to the reciprocal of the previous approximation Φ(n). This gives a formula Φ(n+1) = 1+ 1/Φ(n). Now we substitute the successive values of Φ(n) in the formula repeatedly to build up a sequence of continued fractions. The limit of these continued fractions as n goes to infinity is phi.

For nested radicals expression, take a look at the property in #1. The equation Φ^2  = 1 + Φ likewise produces the continued square root.

Image courtesy of http://www.goldennumber.net, Gary B. Meisner.

Other than these amazing properties, Phi is connected to other mathematics. Most notable link is Fibonacci sequence, discovered by Leonardo Fibonacci, an Italian mathematician, in 1175 AD, but it is a mystery if Fibonacci was aware of the link between what he had discovered and Phi.

The Fibonacci sequence is defined recursively. It starts off with two ones, and each successive term is the sum of the two terms before it. So the Fibonacci numbers are 1, 1, 2, 3, 5, 8, 13, 21, 34,… Johannes Kepler who showed that the Golden Ratio is the limit of the ratios of successive terms of the Fibonacci sequence. If we take the ratio of two successive numbers and continue on the fractions, we can see that ratios are getting very close to Phi.

2/1 = 2

3/2 = 1.5

5/3 = 1.666666…

8/5 = 1.6

13/8 = 1.625

…

233/144 = 1.618055556…

377/233 = 1.618025751…

The fractions of Fibonacci numbers give values that are alternatively higher and lower than Phi, and converge on Phi as the number increases. So the limit of F(n+1)/F(n) when n is approaching to infinity is equal to Phi.

Image: Wikimedia Commons.

It is not only mathematics that connects Phi and Fibonacci. The spiraling growth of leaves, flower petals, and seed pods follows Phi rotation. This minimizes the amount of overlap of any leaf by those leaves located higher on the stem, which allows each leaf to receive the maximum amount of sunlight for photosynthesis. So it is not a coincidence that Fibonacci numbers are commonly found in the plant’s spiral growth pattern of new cells because they essentially express the Phi ratio. Although it is not absolutely true for all plant species, both Phi and Fibonacci explain intricate and sophisticated patterns found in nature. Phi is amazingly connected to every parts of the world, which explains why its reference is so ubiquitous in a variety of areas such as arts, architectures, and mathematics. It has played a significant role in deeper understanding of life and universe, and I think it is why people often call it “the fingerprint of God.”

sources

https://archive.org/details/euclid_heath_2nd_ed

Mathematics of Phi, 1.618, the Golden Number

http://mathworld.wolfram.com/GoldenRatio.html

http://jwilson.coe.uga.edu/emt669/student.folders/frietag.mark/homepage/goldenratio/goldenratio.html

http://nrich.maths.org/2737

The Golden Ratio

Often times, students ask themselves, “How will this apply to me in the real world?”, or  “I never use math, why do I have to learn this?”. Doubt may exist about the usefulness of mathematics, but there is no evidence that supports this doubt. As a student studying math in higher education, I know that math is all around us. I know that everything relies, and consists of some form of mathematics. The most prevalent discovery of math, that is both commonly seen, and unseen, is the Golden Ratio.  The reason I say the Golden Ration is the most prevalent, is because it can be found in nature, science, architecture, and most other aspects of life.

The golden ratio is a number found by dividing a line into two parts, say A and B. The segment A would be longer than segment B, and when A is divided by B, it is equal to the whole length of the line divided by A. The golden ratio is numerically defined as the number 1.6810339887498948420…., and continues on into infinity. It is also represented by the greek letter phi. The golden ratio has been found in nature, and the physical universe. It is not known when it was first discovered by mankind, but can be seen in the works of man dating from ancient times.

The human face is an example of how the golden ratio can be found in nature. When looking at the face, the mouth and nose are positioned in between the eyes and the chin, which represents a golden section. A “perfect” face will have golden proportions between the length and width of the face, the length of the lips and the width of the nose, and the distance between pupils and the eyebrows. Even though all humans are unique, the average of these distances between features is close to phi. It has also been said, that the closer ones features adhere to phi, the more “attractive” society finds them. The reason being, as originally stated, is because the golden ratio is thought to be the most pleasant to the eye. We can even find the golden ratio in our DNA. The molecules in our DNA have been measured to be 34 angstroms in length, and 21 angstroms wide at each full cycle of its double helix spiral.

Parthenon, Athens, Greece The Parthenon without tourists! Athens, Greece (1989/379) From flickr.com, posted by GothPhil

Architecture is another place where the golden ratio is put to use. One example is the Parthenon, found in Athens, Greece. The length and height of the structure,  the spacing between the columns, and the tip of the roof are all contained in the golden ratio. Within the building many golden rectangles can be found as well. The dimensions of the Great Pyramid of Giza, in Egypt, is also based off the golden ratio. The Egyptians believed the golden ratio to be sacred, and it was an important part of their religion. For the Pyramid of Giza, the ratio of the height of the slant compared to one half the length of the base, is the golden ratio. In modern architecture, the golden ratio still applies. In Toronto, Canada stands the CN tower. The CN tower is the tallest freestanding structure in the world. The observation deck of the tower is found at 342 meters, where the total height is 553.33 meters. This ratio between these two lengths is 0.618, or phi.

Not only is the golden ratio used for architecture and design, but also for beauty. Artists for centuries have applied the golden ratio to their work to create the most beautiful pieces of art known to the world. These examples are found in pieces such as The Last Supper by Leonardo Da Vinci, the ceiling of the Sistine Chapel by Michelangelo, and Bathers by Seurat. In the painting of The Last Supper, Leonardo Da Vinci used the golden ratio determine where Christ would sit in relation to the table, and his apostles, as well as, the proportions between the walls and the windows. The golden ratio can be found on the ceiling of the Sistine Chapel where the finger of God, and the finger of Adam meet.  This point, is found by taking the ratio of the height, and width of the area that they are contained in. All of these works of art apply the golden ratio to convey the most realistic shapes and dimensions.

The next time someone says that math does not apply to them or the real world, I would simply suggest they look in the mirror, or visit the nearest museum. The golden ratio can be found in all aspects of life, and will continue to be used to improve the beauty of our surroundings. As humans, we desire organization and structure in our lives. Math provides such needs, and the golden ratio is just one method that is used universally.

Sources:

https://www.dartmouth.edu/~matc/math5.geometry/unit2/unit2.html#Great Pyramid

http://www.geom.uiuc.edu/~demo5337/s97b/art.htm

Golden Ratio in Art Composition and Design

http://io9.com/5985588/15-uncanny-examples-of-the-golden-ratio-in-nature

http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html

http://www.livescience.com/37704-phi-golden-ratio.html

The Golden Ratio is All Around You

You have been told from the time you started school that math was important because math is everywhere. Did you ever believe that? The point of this post is to prove that statement. Math is everywhere, specifically the golden ratio.

The golden ratio is Φ  = (1 + √5) /2 = 1.61803398874989484820. “This “golden” number, 1.61803399, represented by the Greek letter Phi, is known as the Golden Ratio, Golden Number, Golden Proportion, Golden Mean, Golden Section, Divine Proportion and Divine Section.”¹ This number was written about by Euclid in “Elements” around 300 B.C., by Luca Pacioli, a contemporary of Leonardo Da Vinci, in “De Divina Proportione” in 1509, by Johannes Kepler around 1600, and by Dan Brown in 2003 in his best selling novel, “The Da Vinci Code.”¹

The golden ratio is obviously found in the world of mathematics. The golden ratio is created when one can divide a line in a unique way. Imagine being presented with a wooden plank to cut. Where should I make the cut? There is one unique place you could cut that would give you the golden ratio. This mean that the ratio of the larger piece to the smaller piece is the same ratio as the larger piece to the entire plank prior to being cut. We could then cut that smaller piece at a certain point and get a piece one and piece two such that the ratio of piece one to piece two is the same ratio as piece two to the whole smaller piece. And the process could continue. So what makes that so special? It is special because this proportion doesn’t just appear in mathematics; it appears in your body, nature, architecture, and the solar system.

Nature and Life

Think of an ant or search of an image for an ant. Their bodies seem a bit odd at first, but look closer. An ant’s body has been distributed by the golden ratio. Think of a moth or a butterfly. In order for their wings to do what they do, they have been distributed in the golden ratio. Think of a snail’s shell or the classic spiral seashell. How is it that the shell can look like a never-ending spiral? It is because that shell uses the golden ratio. Look at your neighbor. The torso to leg, the head to the torso, the sections of your fingers; all of these are examples of the golden ratios in your own body.

Image courtesy of http://www.goldennumber.net, Gary B. Meisner, Copyright 2001-2013.

It was always said that beauty is in the eye of the beholder, but is that really true? What if I told you that beauty was based on the golden ratio? Would you believe me? There is sound basis in scientific study and evidence to support that what we perceive as beauty in women and men is based on how closely the proportions of facial and body dimensions come to Phi.² “For this reason, Phi is applied in both facial plastic surgery and cosmetic dentistry as a guide to achieving the most natural and beautiful results in facial features and appearance.”²

Image courtesy of http://www.goldennumber.net, Gary B. Meisner, Copyright 2001-2013.

Art and Design

Because of the constant presence of phi in nature, we, as a civilization, have brought the golden ratio into many of our masterpieces in art. Consider the Egyptian Pyramids. It is said that the ratio between the height, base, and hypotenuse is the golden ratio. Greeks were aware of the golden ratio when they built the Parthenon.¹ It is quite obvious if you have seen the movie, The Da Vinci Code, that Leonardo Da Vinci used phi in his classic drawings. The painting of the Last Supper used the golden ratio to determine the placement of Christ and the disciples to the table, walls, and windows around them.¹

Image courtesy of http://www.goldennumber.net, Gary B. Meisner, Copyright 2001-2013.

The golden proportion is in places where we would never imagine. Next time you buy a bottle of Pepsi, look very critically. How did they decide where to but the circular logo or how big to make the logo or to what proportion the writing should be to the logo? These questions are answered by using the golden ratio. “It’s even being used in high fashion clothing design, such as in the “Phi Collection” announced in 2004 and covered by Vogue, Elle and Vanity Fair.”¹

Image courtesy of http://www.goldennumber.net, Gary B. Meisner, Copyright 2001-2013.

Do You Believe Me Now?

“In matters of reason, seeing is believing but in matters of faith, it is believing that first opens the door to seeing. The best way to know for yourself where Phi is present and where it is imagined is to explore with an open mind, learn and reach your own conclusions.”¹This post was created to open your eyes to being critical of how things came to be around you. One can always ask the questions “Why?”. I challenge you to ask that question and play with the idea that the golden ratio may be the answer. Your opinion is your own. I can only present you with articles that either support or deny the importance of the golden ratio. This particular post was in support of its importance, but please feel free to read the following article that has a difference perspective. http://www.umcs.maine.edu/~markov/GoldenRatio.pdf

Sources:

Meisner, Gary B. (2014, May). Article title. Phi: The Golden Number, September 2014, from     http://www.goldennumber.net

The Divine Proportion : A Study in Mathematical Beauty by H. E. Huntley