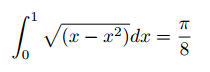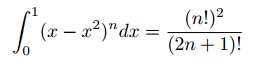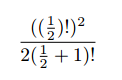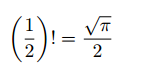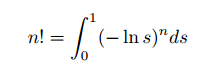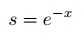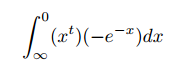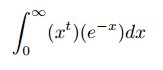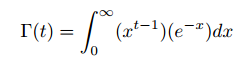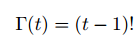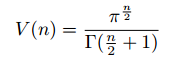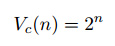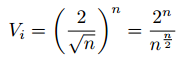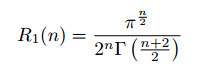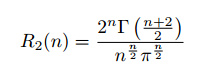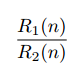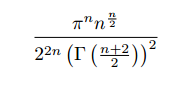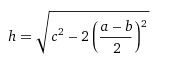Three Centers of a Triangle

There’s far too little geometry—excluding topology and non-Euclidean stuff—on this blog, so let’s add a little.

Euler line HU. Points H, U, and S are
respectively the circumcenter, centroid,
and orthocenter. Image: Rene Grothmann at the German Language Wikipedia.

Our goal is to get to the Euler line, a line that passes through a triangle’s circumcenter, centroid, and orthocenter. The line is only determined for non-equilateral triangles; the points coincide in the equilateral case. We’ll look at the three points above.

The circumcenter, centroid, and orthocenter are all “centers” of triangle. But what is a center of a triangle? Surely, it’s not a point equidistant to all points on the triangle. Our triangle would be a circle in that case.

The circumcenter of a triangle ABC is the center O of the circle K that triangle ABC is inscribed in.

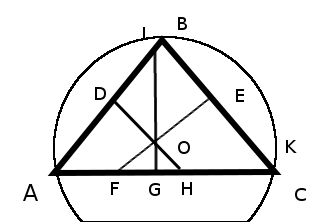
Circumcenter O of triangle ABC. Image drawn by me.

The circumcenter is actually the intersection of the three perpendicular bisectors of the triangle: FE, IG, and DH. To see this, first suppose that triangle ABC has a circumscribed circle K with center O. Draw radii AO, BO, and CO to each of the triangles vertices. This creates three smaller triangles AOB, BOC, and AOC. In each of these smaller triangles, drop an altitude from O. For example, in triangle AOB, altitude OD would be dropped. This splits AOB into two smaller triangles that are congruent by SAS, Line OD is perpendicular to AB by construction, and AD = DB. Hence OD is indeed a perpendicular bisector of side AB. Repeating this for other sides shows that the center of the circumscribed circle is the intersection of ABC‘s perpendicular bisectors.

Moreover, the intersection of any to perpendicular bisectors is equidistant from each of the triangle’s vertices. The reader can see this by considering triangle AOC. Perpendicular bisector IG splits AOC into triangles that are congruent by SAS. It follows that lengths AO and OC are equal. Repeat for the other sides. We then see that the intersection of the perpendicular bisectors is equidistant from the triangle’s vertices. Thus the perpendicular bisectors of a triangle uniquely determine its circumcenter.

The centroid is the intersection of a triangle’s three medians, lines drawn from a vertex that bisect the opposite side. As said in class, the centroid is the center of mass for a thin, triangular solid with uniformly distributed mass.

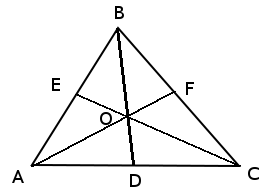
Centroid O of triangle ABC. Drawn by me.

The reader may suspect whether the three medians of a triangle intersect. Clearly two of the medians intersect; otherwise our triangle ABC would be a line. But the full proof is a little tedious. The proof involves assuming that two medians AF and CE intersect and drawing a parallelogram using the midpoints of the medians. We link to some proofs: http://jwilson.coe.uga.edu/EMAT6680Fa06/Chitsonga/MEDIAN/THE%20MEDIANS%20OF%20A%20TRIANGLE.htm uses classical geometry and http://math.stackexchange.com/questions/432143/prove-analytically-the-medians-of-a-triangle-intersect-in-a-trisection-point-of uses vectors.

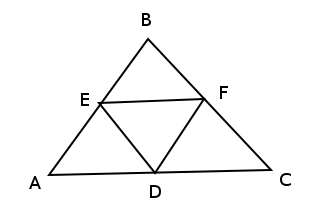
Four congruent triangles using midpoints. Image drawn by me.

Interestingly, the midpoints of the sides of triangle ABC—the ends of the medians—cut the triangle into four congruent triangles. We will prove this in a roundabout way. Let E be the midpoint of AB. Draw a line EF parallel to AC where F intersects BC. Similarly draw FD parallel to AB. By construction, EFDA and EFCD are parallelograms. Then AD = EF = DC, so D is the midpoint of AC. Similarly, F is the midpoint of BC. The reader can see that the triangles are congruent by repeatedly applying SAS.

Our final center is the orthocenter, the intersection of the three altitudes of a triangle. An altitude is a segment drawn from a vertex that is perpendicular to the opposite side. As with the two previous centers, the intersection of the altitudes at a single point isn’t immediately obvious.

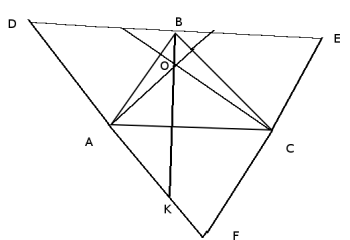
Orthocenter O of triangle ABC. Drawn by me.

We show that the altitudes of triangle ABC intersect. Construct triangle DEF with triangle ABC inscribed in it by making sides DF, FE, and DE parallel respectively to BC, AB, and AC. Draw altitude BK where K intersects DF. Since AC is parallel to DE, BK is perpendicular to DE. Moreover, ADBC and BACE are parallelograms, so DB = AC = AE. Hence BK is a perpendicular bisector of DE. We repeat the argument for the other altitudes of triangle ABC. Then the altitudes of ABC intersect because the perpendicular bisectors of DEF intersect.

There are a few other centers of a triangle that are either irrelevant to the Euler line or take too long to construct (i.e. I’m tired of drawing diagrams). The incenter is the center of the circle inscribed within a triangle. The incenter also turns out to be the center of a triangle’s angle bisectors. The Euler line doesn’t pass through the incenter.

The nine-point circle is the circle that passes through the feet of the altitudes (the end that isn’t the vertex) of a triangle.

Nine-point circle of ABC. Image: Maksim, via Wikimedia Commons.

Strangely, the circle also passes through the midpoints of the sides of its triangle. But that’s not all. The circle passes through the Euler points, the midpoints of the segments joining the triangle’s vertices to the triangle’s orthocenter. Thus the nine-point circle does indeed pass through nine special points of a triangle. The center of the nine-point circle lies on the Euler line.

After all this, we still haven’t proved that the circumcenter, centroid, and orthocenter lie on the same line. We won’t prove this. Here’s a video of the proof by Salman Khan: https://www.youtube.com/watch?v=t_EgAi574sM. The proof uses a few facts about the centers we haven’t discussed, but these facts aren’t too hard to show. Refer back to my four congruent triangles picture. Let O, K, and L respectively be the circumcenter, centroid, and orthocenter of triangle ABC. Then Khan proves that triangle DOK is similar to triangle BLK. This implies angles DKO and CKL are equal, which means O, K, and L lie on the same line.

Sources and cool stuff:

H.S.M. Coxeter and Samuel L. Greitzer’s Geometry Revisited

Paul Zeitz’s The Art and Craft of Problem Solving (Chapter 8 is called “Geometry for Americans”)

Wolfram on the nine-point circle: http://mathworld.wolfram.com/Nine-PointCircle.html

A fun way to play with the Euler line: http://www.mathopenref.com/eulerline.html

Khan’s Euler line video: https://www.youtube.com/watch?v=t_EgAi574sM

Wolfram on the Euler line: http://mathworld.wolfram.com/EulerLine.html

Classical median proof: http://jwilson.coe.uga.edu/EMAT6680Fa06/Chitsonga/MEDIAN/THE%20MEDIANS%20OF%20A%20TRIANGLE.htm

Vector median proof: http://math.stackexchange.com/questions/432143/prove-analytically-the-medians-of-a-triangle-intersect-in-a-trisection-point-of

Euler’s Gamma Function and Ball/Cube Peg/Hole Problem

n!

No, I’m not really excited about the letter n. f(n) = n! is the factorial function. Taking the factorial of a positive integer n can be defined as follows:

n(n-1)(n-2)…(3)(2)(1)

A graph of the gamma function. Image: public domain, via Wikimedia Commons.

Factorial has its uses in many areas of mathematics. Counting, permutations, the “n choose m” algorithm – all utilize factorial to a certain extent. Like me, some of you may have wondered why factorial cannot be extended to more than just the positive integers. Leonhard Euler’s gamma function resolves this problem.

John Wallis, who lived primarily in the 17th century, took the first steps in defining factorial outside of the positive integers. He knew the following two integrals were true:

Using the second formula and picking n = ¹/₂ (to match the first integral) yields:

Solving for ¹/₂ ! reveals the following:

This means that, assuming factorial can be defined outside of positive integers, ¹/₂ ! should be equal to ^√π/₂.

In 1730, in a letter to Christian Goldbach, Euler defined n factorial for positive real numbers.

If we replace n by t (signifying that n doesn’t have to be a natural number), and do the substitution x = -ln(s), we get the following:

The bound 0 becomes ∞ and the bound 1 becomes 0. Completing the substitution, we get this integral:

Flipping the bounds so the smaller is the on the bottom requires multiplying by negative one.

Mathematicians have defined the gamma function to shift the input variable down by one, so the modern gamma function (for positive values of t) is the following:

If t is a positive integer, it can be defined more simply as follows:

One interesting application of the Gamma function is the question, “Does a round peg fit better in a square hole than a square peg in a round hole?” This question can be simplified to a matter of ratios. That is, is the ratio of the area of the circle to that of the circumscribed square or the ratio of the area of the square to that of the circumscribed circle bigger? This question was considered by Jeffrey Nunemacher in 1986 in his article The Largest Unit Ball in any Euclidean Space. It laid the framework for Joel Azose’s work on it in his work, On the Gamma Function and its Applications. Azose used the following method to solve the problem using the gamma function.

If we expand the problem to the nth dimension, then the volume of the unit “n-ball” (a 2-ball would be a circle, a 3-ball a sphere) is as follows:

Because the side length of a circumscribed n-cube (a 2-cube would be a square, a 3-cube a cube) is equal to the diameter of the n-ball, the volume of our circumscribed n-cube is:

Because the diagonal of an inscribed n-cube is equal to √n times its edge as well as being the diameter of the circle, a side of the inscribed n-cube is ²/_√n. Therefore its volume is:

If the ratio of the volume of the n-ball to the volume of the circumscribed n-cube is R₁(n) and the ratio of the volume of the inscribed n-cube to the volume of the n-ball is R₂(n), we get:

We can then take the ratio of R₁ to R₂, which is:

The ratio simplifies to this:

As n approaches infinity, the ratio approaches zero. This is true because 2²ⁿ easily outgrows π^n/2, and although it is not obvious, the gamma function easily outgrows n^n/2 when it is squared. Therefore, the denominator grows much more quickly than the numerator for large n, so the limit as n approches infinity is zero. This means that for sufficiently high values of n, the n-cube fits the n-ball better than the n-ball fits the n-cube. As it turns out, this is true for n≥9.

The gamma function is certainly one of the most interesting single variable functions I have seen in mathematics. Its graph seems very unusual, and it visually appears to contain parts of other functions’ graphs. I haven’t researched many applications, but this is definitely one of the more interesting ones I found. Plus, it has answered my question: what if the factorial function could take non integer inputs?

References:

https://en.wikipedia.org/wiki/Gamma_function

Click to access joel.pdf

Transcendental Numbers: Beyond Algebra

The history of mathematics has been fraught with disappointments for mathematicians. This is particularly true in regard to the expected and continued failure of numbers, and math in general, to be pure and graceful. The Pythagoreans, in 6^th century BCE Greece, venerated the whole numbers with an almost religious devotion because of their purity, and believed that the universe could be described by using only whole numbers. Unfortunately, math is not as pure as the Pythagoreans thought, which was revealed first by Hippasus of Metapontum when he discovered an undeniable proof for the existence of irrational numbers. Incidentally, Pythagoras had poor Hippasus drowned because of this. (The tale of the drowning of Hippasus may be merely a legend, like much of what is “known” about the Pythagoreans, due to a lack of reliable sources from the period.) Another impurity of numbers was wrestled with for millennia in the form of the square roots of negative numbers, a problem that was only put to rest with the advent of the imaginary number i. However, numbers turned out to be even weirder than previously imagined, because transcendental numbers were discovered by Gottfried Wilhelm Leibniz, in 1682.

In order to understand transcendental numbers, we need to understand algebraic numbers, or numbers that are not transcendental. An algebraic number is any number that is the solution to a polynomial with rational coefficients. Rational numbers are numbers that can be written as the ratio of two integers. All rational numbers are algebraic numbers, for instance the number 2 is a rational number because it can be written as 2/1. It is also an algebraic number because it is the root of the polynomial X – 2 = 0, which is a polynomial with only rational coefficients. While all rational numbers are algebraic, not all are algebraic numbers are rational, for example, √ (2) is an irrational number, but it is also algebraic because it is the solution to X² – 2 = 0. Strangely, the imaginary number i, although it is not real, is an algebraic number since it is the root of the polynomial X² + 1 = 0.

Transcendental numbers are numbers that cannot be written as the root to a polynomial with rational coefficients. All transcendental numbers are irrational. Leibniz coined the term “transcendental” in his 1682 paper in which he proved that the sin function is not an algebraic function.  Leonhard Euler (1707- 1783) was the first to generally define transcendental numbers in the modern sense, although it was Joseph Liouville, in 1844, who definitively proved the existence of the first transcendental number. That number is now called the Liouville Constant, and it is .110001000… with a 1 in every n! place after the decimal. The Liouville Constant was specifically constructed by Liouville to be a transcendental number. However, Charles Hermite first identified a transcendental number that was not created for that purpose in 1873. That number was the constant e, or Euler’s number, and is the base of the natural logarithm.

A famous transcendental number, called “Champernowne’s Number,” was discovered in 1933 and named after David G. Champernowne. It is formed by concatenating all the natural numbers behind the decimal point 0.12345678910…. Although, easily the most famous transcendental number is pi, which was proved to be transcendental by Ferdinand von Lindemann in 1882.

Pi. Image: Travis Morgan, via Flickr.

Georg Cantor, in the1870’s, proved that there are as many transcendental numbers as real numbers, a concept that is mind-boggling since the real numbers are uncountable. However, only a few numbers have ever been definitively proven to be transcendental, because it is extremely difficult to prove that any given number is transcendental.

Along with irrational and imaginary numbers, transcendental numbers have challenged and frustrated mathematicians throughout the ages. Undoubtedly, Pythagoras would be horrified by transcendental numbers, or maybe he would just drown anyone who tried to tell him about them. Today, however, transcendental numbers are embraced by mathematicians as a deep and important part of math.

Sources:

https://www.flickr.com/photos/morgantj/5575500301/in/photolist

http://nrich.maths.org/2671

http://individual.utoronto.ca/brucejpetrie/dissertation.html

http://sprott.physics.wisc.edu/pickover/trans.html

http://education-portal.com/academy/lesson/algebraic-numbers-and-transcendental-numbers.html

http://transcendence.co/transcendental-numbers/

http://www.daviddarling.info/encyclopedia/C/Champernownes_Number.html

http://www.britannica.com/EBchecked/topic/485235/Pythagoreanism

Use Your i-M-A-G-i-N-A-T-i-O-N

It’s kind of embarrassing to admit this as a 24-year-old college student, but I have an imaginary friend. His name is √(-1). He doesn’t keep it as real as some of my other friends, but he’s always my main dude in some of the more complex friendships I get involved in. He’s got a pretty interesting life story, and he’s exceptionally old and wise (imaginary friends never die). He was birthed by the Greek mathematician Heron of Alexandria in the first century A.D. He had a rough childhood (neglected and completely ignored by his father), partially because no one understood him. People ignored him, calling him useless. His name was even meant to be derogatory at one point.⁴  √(-1) met Gerolamo Cardano (coined the term “imaginary”), his first true friend, in 1637. After Cardano passed away, √(-1) was lonely until he was accepted into a new circle of friends during the 1700 and 1800s: Leonhard Euler, Carl Gauss, and Caspar Wessel. Although his new friends were a little on the nerdy side, they helped restore his personal image – eventually helping him to become a internationally known, and well respected celebrity.

Image: Matheepan Panchalingam, via Flickr.

Okay, enough with my weird metaphorical stories. I’m here to tell you all about imaginary numbers. Now although the previous paragraph was strange and pretty corny, a lot of truth resides within. Heron of Alexandria was the first known person to have encountered imaginary numbers, back in the first century A.D.¹ He has been called a Greek mathematician, but interestingly enough, we now believe he may have actually been Egyptian.¹ So, how did Heron, the father of imaginary numbers, make such an important discovery? Well, he was trying to find the volume of a frustum of a pyramid with a square base. Specifically a pyramid with a side of the lower base is 28, of the upper 4, and the edge 15. Now the formula to solve this problem, as noted in the Stereometria of Heron of Alexandria is:

Using a = 28, b = 4, and c = 15, Heron ultimately reduced this problem to equal √(81 – 144). However instead of writing h = √(-63), he wrote h = √(63).¹  Now whether Heron did this intentionally or not, we’ll never know. What we do know is this: No other scholar even bothered to take notice of these imaginary numbers for at least a thousand years. Believe it or not, from here it took another five hundred years for scholars to start taking imaginary numbers seriously.¹

The Italian engineer and architect Rafael Bombelli started searching for solutions to cubic equations in 1572, and during that time, he started defining some guidelines for using imaginary numbers.⁵ At this point, most mathematicians didn’t want to believe these numbers were significant, or that they even existed. Bombelli’s “wild idea” – that you could multiply imaginary numbers and end up with a real solution, didn’t sit well with fellow scholars. In fact, Bombelli didn’t even think imaginary numbers could ever have a true purpose, he just viewed them as a useful artifact to solve his equations. Later on, along came Leonhard Euler, a math rockstar in many people’s eyes. Euler really takes the cake here for noticing one of math’s more bizarre imaginary (in a math sense) equations. He showed the world how closely i, e, and π are related and further convinced the math community that i was relevant:² Today, this is known as Euler’s identity.

e^iπ = cosπ +i(sinπ) 

Which reduces to:

e^iπ = -1 + 0i 

In simpler terms:

e^iπ = -1

In 1842 Carl Gauss did the impossible. He actually defined imaginary numbers (although Cardano coined the term “imaginary”.). Later on, once the reality of i was more widely accepted, our understanding mathematics expanded greatly. Euler, Gauss, and Wessel (1700s and 1800s) utilized imaginary numbers and led to the creation of complex numbers, which have a vital importance in math/science today.

Complex Numbers:

Instead of describing numbers and algebraic equations as points on a line, complex numbers and equations become points on a plane. Numbers are two dimensional – just like the integer “1″ is the unit distance on the axis of the “real” numbers, “i ” is the unit distance on the axis of the “imaginary” numbers. This results (in general) in complex numbers: They consist of two components, defining their position relative to those two axes. We generally write them as “a + bi ” where “a” is the real component, and “b” is the imaginary component.⁴

A basic graph showing real and imaginary points making up a complex line. Image: Public Domain.

Let me simplify this for you – What this means is that every polynomial equation has roots. Specifically, a polynomial equation in “x” with maximum exponent “n” will always have exactly “n” complex roots.

Me, myself, and i :

Imaginary numbers are more prevalent in the world than you’d think. Without the electronic circuit theories conceived from imaginary numbers, I wouldn’t be typing this blog post, and more importantly, you wouldn’t be reading it. When we plug something into an electrical outlet, we just expect our electronic devices to receive power. In fact, I bet you plugged in your laptop charger today and didn’t even think twice about it. What does exactly does this AC power have to do with imaginary numbers? Everything.

Voltage can be viewed as the amount of force pushing the current through your laptop charger and ultimately into your laptop’s battery. Voltage is a complex number. In fact, if you have a voltage of 110 volts AC at 60 hz (US Standard), that means is that the voltage is a number of magnitude 110. If you were to plot the “real” voltage on a graph with time on the X axis and voltage of the Y, you’d see a basic sine wave. Take the graph below for example:

Basic sine wave showing only real voltage. Image: Public Domain.

If you decided to put your key in the outlet when the voltage was supposedly zero on the real portion of that graph, you’d still get electrocuted. That’s right, even though real voltage is zero here, “imaginary” electricity can give you quite a shock.³ Take the moment marked t1 on the above graph for example. The voltage at time t1 on the complex plane is a point at 110 on the real axis. At time t2, the voltage on the “real” axis is zero – but on the imaginary axis it’s 110. In fact, the magnitude of the voltage is always constant at 110 volts, and this is an important fact to know.⁵  All our modern day electronics account for these weird voltage patterns, and strangely enough this imaginary unit is represented with a  “j ” rather than an i (“i ” is used to represent current)!³

All in all, you can thank Bombelli and Euler for introducing imaginary numbers. Not only do they make math more confusing, but they also have many crucial applications in the world around us today.

Sources:

1. http://press.princeton.edu/chapters/i9259.pdf 
2. http://www.mathsisfun.com/numbers/imaginary-numbers.html
3. http://en.wikipedia.org/wiki/Electrical_impedance
4. http://en.wikipedia.org/wiki/Imaginary_number
5. http://scienceblogs.com/goodmath/2006/08/01/i/

Math Tricks and Fermat’s Little Theorem

So you think you’re a math whiz. You storm into parties armed with math’s most flamboyant tricks. You can recite the digits of π and e to 50 digits—whether in base 10 or 12. You can calculate squares with ease, since you’ve mastered the difference of squares x² – y² = (x + y)(x – y). In tackling 57², simply notice that 57² – 7² = (57 + 7)(57 – 7) = 64*50 = 3200. Adding 7² to both sides gives 57² = 3249.

Image by Hashir Milhan from
Wikimedia Commons under
Creative Commons.

You can also approximate square roots using the truncated Taylor series √x ≈ c + (x – c²)/(2c) where c² is the closest perfect square less than or equal to x. So √17 ≈ 4 + (17 – 16)/(2*4) = 4.125, whereas √17 = 4.123105 . . ..

But do you know what number theory is? It’s not taught in high school, and everyone’s repertoire of math tricks needs some number theory. Mastering modular arithmetic—the first step in number theory—will make you the life of the party. Calculating 83 mod 7 just means find the remainder after dividing by 7: 83 = 11*7 + 6, so 83 ≡ 6 mod 7. But it’s actually easier since 83 = 7*12 + (-1), so 83 ≡ -1 ≡ 6 mod 7. Modular arithmetic reveals the secrets of divisibility. Everybody knows the trick to see whether 3 divides a number; you just add the digits and check if 3 divides that number. But the reasoning is obvious when you write m = 10ⁿa_n + 10^n-1a_n-1 + . . . + 10a₁ + a₀ where the a_i are the digits of m. Each 10^k has a remainder of 1 modulo 3 so m ≡ a_n + a_n-1 + . . . + a₁ + a₀ mod 3. Using this method generates tricks for other integers.

For instance, if 13 divides m, then 13 divides a₀ – 3a₁ – 4a₂ – a₃ + 3a₄ + 4a₅ + a₆ – 3a₇ – 4a₈  + . . . and the pattern continues. This is because

10 ≡ -3 mod 13,

10² ≡ 10*10 ≡ (-3)(-3) ≡ 9 ≡ -4 mod 13,

10³ ≡ 10²*10 ≡ (-4)(-3) ≡ 12 ≡ -1 mod 13,

10⁴ ≡ 10³*10 ≡ (-1)*(-3) ≡ 3 mod 13,

10⁵ ≡ 10⁴*10 ≡ 3*(-3) ≡ -9 ≡ 4 mod 13,

and 10⁶ ≡ 10⁵*10 ≡ 4*(-3) ≡ -12 ≡ 1 mod 13.

From 10⁶ and onwards the pattern repeats. In fact, calculating 10ⁿ mod k for successive n will reveal the divisibility rule for k.

Then comes Fermat’s little theorem, the key to solving seemingly impossible calculations.

Fermat. Image from Wikimedia
Commons. Under public domain.

The theorem states for a prime p and integer a that a^p ≡ a mod p. If p doesn’t divide a, then  a^{p -1} ≡ 1 mod p. I’ll illustrate the power of this little result in a computation. Let’s find 2³⁷¹ mod 5. We’ll be using 2⁴ ≡ 1 mod 5, which we get from Fermat’s little theorem. Now 2³⁷¹ = 2³⁶⁸2³ =(2⁴)⁹²2³, so by the theorem, 2³⁷¹ = (2⁴)⁹²2³ ≡ 1⁹²2³ ≡ 1*2³ ≡ 8 ≡ 3 mod 5. Exploiting Fermat’s little theorem can impress your friends, but try to avoid questions. Computing residues modulo a composite number—calculating b mod n for a composite number n—may require paper and ruin the magic.

Leonhard Euler proved a more general version of Fermat’s little theorem; it’s called the Euler-Fermat theorem. This theorem isn’t for parties; explaining it to the non-mathematically inclined will always require paper and some time. Nonetheless, it will impress at dinner if you have a napkin and pen.

Understanding this theorem requires Euler’s totient function φ(n).

Euler. From Wikimedia
Commons. Under public domain.

The number φ(n) for some n is the number of positive integers coprime with n that are less than or equal to n. Two numbers a and b are coprime if their greatest common factor is one. Hence 14 and 3 are coprime because their biggest shared factor is 1, but 21 and 14 aren’t coprime because they have a common divisor of 7. Moreover, φ(14) = 6 because 14 has six numbers less than or equal to it that are coprime with it: 1, 3, 5, 9, 11, and 13. Notice that if p is prime, φ(p) = p – 1 because every number less than p is coprime with p.

Now the Euler-Fermat theorem states that a^φ(n) ≡ 1 mod n, which looks similar to a^{p -1} ≡ 1 mod p for a prime p. In fact, if n = φ(p) = p – 1 for a prime p, the theorem reduces to Fermat’s little theorem.

Fermat’s little theorem has another generalization, Lagrange’s theorem. Joseph-Louis Lagrange was Euler’s student. Lagrange’s theorem generalizes both the previous theorems and doesn’t even require numbers. But due to the required background in group theory, I won’t go over the theorem. You can find links to more information on Lagrange’s theorem below.

Remember, a math whiz doesn’t need props like a magician does. Hook your audience with some modular arithmetic, and reel the people in with Fermat’s little theorem. If you want to get complicated, the most you’ll need is a pen and some paper.

Sources and cool stuff:

Math tricks: http://www.businessinsider.com/x-math-party-tricks-that-will-make-you-a-rockstar-2013-6?op=1

Modular arithmetic: http://nrich.maths.org/4350

Proof of Fermat’s little theorem: https://primes.utm.edu/notes/proofs/FermatsLittleTheorem.html

Euler-Fermat theorem and its proof: http://www.artofproblemsolving.com/Wiki/index.php/Euler%27s_Totient_Theorem

Lagrange’s theorem (only for the brave): http://cims.nyu.edu/~kiryl/teaching/aa/les102903.pdf

Fermat’s bio: http://www-history.mcs.st-and.ac.uk/Biographies/Fermat.html

Euler info: https://3010tangents.wordpress.com/2014/10/05/leonhard-euler-eulers-identity-fermats-last-theorem-and-the-basel-problem/

Lagrange’s bio: http://www-history.mcs.st-and.ac.uk/Biographies/Lagrange.html

Number theory textbooks: Gordan Savin’s Numbers, Groups, and Cryptography and George E. Andrews’s Number Theory

Interesting sources of math tricks and problems: Paul Zeitz’s The Art, Craft of Problem Solving and The USSR Olympiad Problem Book, and What is Mathematics by Richard Courant and Herbert Robbins

Graph Theory

Graph theory is a branch of mathematics that looks at the relationship between objects. I know this might sound a little vague, but to get the basic picture of what graph theory is, I’d like to take a look at the following image:

The bridges of Königsberg. Image: Bogdan Giuşcă, via Wikimedia Commons.

The image above is a drawing of the Königsberg bridges, located in Königsberg, Germany in 1736. This problem was the beginning of graph theory and no one even knew it. It can be defined by the following:

The Königsberg bridge problem asks if the seven bridges of the city of Königsberg, formerly in Germany but now known as Kaliningrad and part of Russia, over the river Preger can all be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began.

Proof by Euler

Leonard Euler, in the year 1735, introduced a counter proof to the problem described above. He realized that the only important issues in the problem were the bridge crossing sequences. Using this abstract he created two new terms, “vertex” or “node”, and “edge.” In the above picture each unique landmass would be classified as a vertex, while each bridge is classified as an edge. Euler’s resulting image would look something like the following:

The graph that represents the bridges of Königsberg. Image: Riojajar, via Wikimedia Commons.

The image above is described as a graph. Within a graph, it does not matter the exact location of each node. However, the connection(s) formed between nodes does matter. Edges between nodes can either be curved or straight, because it’s not important to the graph structure, they are simply showing how each object is connected.

Euler then describes the process of his counter proof by first describing what is now known as the “degree” of a node. A degree of a node is described as how many edges it has (one, two, etc.). His proof says that within a connected graph (there can’t be any nodes that are alone, i.e. not connected to any other node) there can be either zero, or two, nodes that have an odd degree. This proof was monumental in his time and was later validated by Carl Hierholzer.

Traveling Salesman Problem

One of most studied graph theory problems in the field of Computer Science is the Traveling Salesman Problem or TSP for short. The basic problem definition states that given a list of cities and the distances between them, find the shortest path between all cities, where each city is visited exactly once and the “salesman” must return to the original city. Currently there are no algorithms that can solve this problem in polynomial time (polynomial time is described as O(n^a), where n is the number of cities and a is a constant integer). Active research in solving this problem and many algorithms come from general heuristic solutions, which are currently the fastest ways to solve the TSP. The TSP is used in many different fields including logistics, transportation and even microchip production.

Unsolved Problem

There is one major unsolved problem in graph theory known as the “Longest path problem.” The problem is described as finding the longest path in a graph, without repeating vertices, by counting the number of edges the path contains. This problem is classified as NP-hard, implying that it cannot be solved in polynomial time or solved at all (this definition of NP is also one of the Millennium Prize Problems, asking if P = NP, check out http://en.wikipedia.org/wiki/P_versus_NP_problem for a quick definition).

Conclusion

Graph theory is a very interesting subject and it has a lot to offer. Many mathematical and computer science problems have been solved using graph theory. I believe that with continued research, it will be known if the “Longest path problem” can be solved. There are many companies such as FedEx and UPS that are very interested in the traveling salesman problem, because it could greatly reduce the amount of fuel used delivering packages, thus reducing global emissions and saving natural resources. I find graph theory to be a very interesting subject and I hope in due time humanity will have all of the answers to graph theory’s most problematic questions.

References

http://plus.maths.org/content/maths-minute-bridges-konigsberg

http://www.math.uwaterloo.ca/tsp/apps/

http://en.wikipedia.org/wiki/Graph_theory

http://mathworld.wolfram.com/LongestPathProblem.html

http://world.mathigon.org/Graph_Theory

Leonhard Euler: Euler’s Identity, Fermat’s Last Theorem, and the Basel Problem

Leonard Euler. Image: public domain, via Wikimedia Commons.

Leonhard Euler was born in 1707 in Basel, Switzerland, and died in 1783. Over the course of his life he published many articles, some related to fields such as physics and astronomy, but many in the field of mathematics. In mathematics, three contributions he made are Euler’s Identity, his work on Fermat’s Last Theorem, and his solution to the Basel problem. Euler’s Identity is part of the mathematical field of Complex Analysis, which involves the application of various mathematical concepts for complex numbers a + bi, where i = √-1. Fermat’s Last Theorem is part of number theory, a field focused on the relationships between numbers, but primarily the integers. The Basel Problem involves summations, an important part of Calculus where it is used to solve difficult integrals, as well as other areas of Mathematics.

One of Euler’s more profound equations is Euler’s Identity, which states that e^iΠ +1 = 0. This is a special case of Euler’s formula, which shows that e^ix = cos(x) + isin(x). Therefore, in the case of Euler’s Identity, x = Π, so e^iΠ = cos(Π) + isin(Π) = -1 + i(0) = -1. By adding 1 to both sides, the standard result of e^iΠ +1 = 0 becomes apparent.

This Identity has been considered by many to be “remarkable” and “among the most beautiful formulas in mathematics” for a variety of reasons. First, it includes both the number one and the number zero, the multiplicative and additive identities. Furthermore, it involves the constant Π, the most fundamental constant in geometry, and e, also known as Euler’s number, which is the base of the natural logarithm and can be used in many real world applications. Finally, there is i, the fundamental imaginary unit equal to the square root of negative one.

Euler also worked on Fermat’s Last Theorem. The theorem states that for the equation xⁿ + yⁿ = zⁿ, there are no non-zero integer solutions for n equal to any value greater than two. Euler, in a letter to his friend Christian Goldbach, claimed to have a proof of the theorem for the case where n is equal to three. However, part of his proof was incorrect. He relied upon proving that for any numbers p and q where p² + 3q² is a cube, there exist numbers a and b where p² + 3q² = (a² + 3b²)³. He incorrectly attempted to prove this using imaginary numbers, and as such invalidated his proof. Despite this, it could still be argued that he proved the case where n equals three as other mathematicians have used some of his other works to correct his mistakes. Additionally, Euler also proved the case of Fermat’s Last Theorem where n is equal to four.

The Basel problem is finding ∑_n=1^∞1⁄_n². Pietro Mengoli, an Italian priest, originally constructed the problem in 1644; in later years, both Jakob Bernoulli and Gottfried Leibniz, two prominent mathematicians of the time, were unable to solve it. This led to the Basel problem becoming a sort of challenge for mathematicians at the time. It is unknown when Euler first began work on the Basel problem; however, in 1731, he calculated an approximation of the first one thousand terms ¹⁄_1² + ¹⁄_2² + ¹⁄_3² + … + ¹⁄_1000². However, we have learned that his approximation of 1.64393 is only accurate to the first two decimal places. Euler continued to develop more and more accurate approximations, eventually ending up with the approximation 1.644934, which is accurate to six decimal places.

In 1734, Euler published his first proof that the Basel problem was in fact equal to ^Π2⁄₆, which he had previously noticed was approximately equal to 1.644934, his most accurate approximation for the Basel problem. However, he made many logical pitfalls in this intial proof, lending it to the criticism of Daniel Bernoulli, a mathematician and one of his contemporaries. In 1741, Euler had completed his final proof, which remedied the problems of the first. I will now show how Euler proved this, using a result from an earlier proof that ^Π2⁄₈ = 1 + ¹⁄₉ + ¹⁄₂₅ + ¹⁄₄₉ + …, which is required for this proof to be valid.

First, Euler expanded the sum and split it into fractions with even and odd denominators ∑_n=1^∞1⁄_n² = (1 + ¹⁄₉ + ¹⁄₂₅ + ¹⁄₄₉ + … ) + (¹⁄₄ + ¹⁄₁₆ + ¹⁄₃₆ + ¹⁄₆₄ + …). He then observed that the sum of fractions with even denominators is equal to one forth of the original sum (1 + ¹⁄₉ + ¹⁄₂₅ + ¹⁄₄₉ + … ) + (¹⁄₄ + ¹⁄₁₆ + ¹⁄₃₆ + ¹⁄₆₄ + …) = (1 + ¹⁄₉ + ¹⁄₂₅ + ¹⁄₄₉ + …) + (¹⁄₄)(1 + ¹⁄₄ + ¹⁄₉ + ¹⁄₁₆ + …). He already knew that the sum of the fractions with odd denomitors was ^Π2⁄₈. He then substitiued it and the original sum (1 + ¹⁄₉ + ¹⁄₂₅ + ¹⁄₄₉ + …) + (¹⁄₄)(1 + ¹⁄₄ + ¹⁄₉ + ¹⁄₁₆ + …) = ^Π2⁄₈ + ¹⁄₄ ∑_n=1^∞1⁄_n². Euler then subtracted one fourth of the original sum from both sides of the equation, and then multiplied both sides by four thirds to get the final value of ^Π2⁄₆. ^Π2⁄₈ + ¹⁄₄ ∑_n=1^∞1⁄_n² –> (³⁄₄)∑_n=1^∞1⁄_n² = ^Π2⁄₈ –> ∑_n=1^∞1⁄_n² = ^Π2⁄₆

The Basel problem is a special case of the p-series ∑_n=1^∞1⁄_n^p where p = 2. While we now know that the series diverges for p less than or equal to 1 and converges for p greater than 1. Euler worked on the p = 3 case, but his brute force approximations (as initially used in the Basel problem) did not yield any values he recognized. In 1978, it was proven that the number the p=3 case converges to is irrational, but nothing is known about the odd values of p greater than 3.

These are but three of Leonhard Euler’s many contributions in the field of Mathematics. I wrote about these three because I find all of them to be very interesting. Euler’s Identity, of course, has the many mathematical constants, and it amazes me how so many can be related in one equation. Fermat’s Last Theorem is perhaps the most infamous problem in Number Theory, as Fermat scribbled it in the margin of a journal, claiming to have an incredible proof but it would not fit in the margin. And The Basel Problem is the only p-series where the exact sum of the series is known.

Sources:

http://www.amt.edu.au/euler.html

http://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/

http://books.google.com/books?id=eIsyLD_bDKkC&pg=PA160#v=onepage&q&f=false

http://www-history.mcs.st-and.ac.uk/HistTopics/Fermat’s_last_theorem.html

Click to access mobilio.pdf

http://www.biography.com/people/leonhard-euler-21342391#early-life-and-education