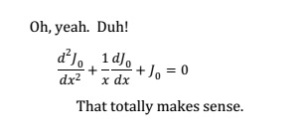The Power of Construction

Eighth grade Geometry was one of my favorite classes. I thoroughly enjoyed the material, as it was unlike anything I had seen in my math education so far. Personally, I felt that Geometry helped combat the classic refrain of nearly every elementary school child of “When am I going to use this”. Geometry had the unique ability to take all of the abstract ideas taught thus far and ground them in the physical world. It was also the first time we were required to write a logical proof, which has been such an important skill to have and understand. However, my favorite part of the class was the constructions.

I clearly remember being excited about buying my very first compass. I knew that with my compass and stainless steel ruler I used as a straightedge, I was ready for anything Geometry could throw at me. In class, we constructed all of the basics: perpendicular bisectors, bisected angles, various regular polygons, and so on. The pentagram construction was my favorite. That knowledge of that construction, combined with chalk, some string, a yardstick and the driveway made for a very interesting conversation with my parents. Construction is a great hands-on approach to math but is rarely seen past the context of 8th grade geometry.

After 8th grade, I never gave it any thought. It wasn’t until my History of Math course that I realized how much power straightedge-and-compass construction really had.

So let us go back to the basics. A straightedge is a ruler without any graduation. It can be used in straightedge-compass constructions to connect two points on a given plane, and extend lines on a given plane. The compass is used to draw circles (that is, a set of all points equidistant from another point), and be able to ‘measure’ a given line segment, and construct that same length elsewhere. So what can you do with this?

As it turns out, quite a bit! For starters, you can do basic arithmetic. Adding just becomes combining two line segments on the same line, and subtraction is the reverse. Multiplication has a geometric representation as similar triangles. If you have a triangle whose base is 1 unit and a hypotenuse of length a, if you draw a similar triangle whose base is length b, the resulting hypotenuse is length ab.

Trisecting a segment. Image: Goldencako, via Wikimedia Commons.

I find this incredible! What took my math educators 8 years to get around to, the Ancient Greeks did right off the bat. They made mathematics immediately tangible and constructible, instead of relying on the esoteric notion of numbers and Algebra. But construction doesn’t stop there. As I’ve mentioned you can create perpendicular lines, create regular polygons, bisect angeles, bisect segments, trisect segments, and more. Given a unit length, you can even construct whole-number measurements of that length, and even some irrationals like square roots. Take this example:

Construction of a square. Image: Aldoaldoz, via Wikimedia Commons.

To construct a regular unit square (all sizes equal to a given unit of measure and all angles are right angles), it’s a simple matter of constructing perpendicular bisectors of segments and measuring with a compass. But can we construct a square that is exactly twice as much area? If the area of a unit square is 11 = 1then the area of a doubled square must be 2. The sides of the square must then be 2 = s2 ; s = 2. To the uninitiated, this might seem like an impossible task! How on earth using a straightedge and a compass can you construct an irrational number? Euclid, however, found a way. Create two lines that are perpendicular to each other. Use the compass to measure out a unit length along each of the two lines, starting from the intersection. This has given you two sides of a right triangle, each with a length of 1 unit. If you connect them an form a hypotenuse, a2+b2= c2; 1 + 1 = c2; c = (1+1) = 2. With this new length as a measurement for your compass, a square with side length 2 is entirely possible.

Euclid did have one problem them though, and that was cube roots. We have shown that doubling the square is possible, but what about doubling the cube? The construction is analogous to the double the square, just with an added dimension. Therefore, if a cube has a volume of 1 cube unit, it’s double should have an volume of 2 cubed units. V = s s s = s3; s = 3V

No matter how hard Euclid tried, he could not construct a cube root. His limitations didn’t stop there. Most famously, he was unable to construct a square the with the area of a circle. This is known as “Squaring the circle.” Again, if we have a circle with the radius of 1 unit, it will have an area of A = r2 =. So to make a square have an area of , we simply have to construct a side with length . Square roots are no problem, it’s just the hypotenuse of a right triangle with sides that sum to . But…how do we sum to with constructions? It turns out, it is impossible. The number is not a “constructible number, ” as they are known, but a “transcendental number.” This wasn’t proved until 1883 by Ferdinand von Lindemann.

While I would never give up the power of algebra and the tools it provides, Euclidean geometry holds a special place in my heart for its sheer physicality. The ability to construct basic arithmetic, regular polygons, and even the odd irrational number grounds math in a way that I think is delayed for far too long in standard Western education. But at least they get around to it.

I end, as always, with wise words from Randall Munroe.

Image: xkcd by Randall Munroe.

Sources

http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Squaring_the_circle.html

http://www.infoplease.com/encyclopedia/world/greek-architecture-ancient-greek-construction-methods.html

http://www.mathopenref.com/constructions.html

“Euclid – Master of us all”

Statue of Euclid in the Oxford Museum of Natural
History, Courtesy of Lawrence OP on Flickr.

After talking about Euclidean and non-Euclidean geometry in class, I wanted to know more about Euclid and his life. I went to a couple different sources, and found an awesome biography from the MacTutor History of Mathmatics archive that gave me a lot of interesting information.

Euclid of Alexandria was born around 325 BC, but we don’t know exactly where he was born. We do know, however, that he died about 265 BC in Alexandria, Egypt. We refer to him as Euclid of Alexandria to avoid confusion with Euclid of Megara, who lived nearly 100 years earlier and was a student of Socrates. (Wikipedia, 2014) We don’t know a whole lot about Euclid’s life. One source of information that exists (although not believed to be very credible) comes from some Arabian authors who claim that Euclid was the son of Naucrates and that he was born in a city called Tyre (present day Lebanon). But, as mentioned, most mathematical historians believe that the claim was invented by the authors. (O’Connor & Robertson, 1999)

Math historians have varying opinions as to the existence of Euclid the mathematician. The most widely held is that Euclid actually was a real person, and that he really did write “The Elements” and the other works published in his name. The second idea is that he was a leader of a team of mathematicians in Alexandria that all contributed in writing the works attributed to Euclid. Some think that this team even continued to publish “The Complete Works of Euclid” in Euclid’s name after his death. The third hypothesis is that Euclid of Alexandria was a creation of this team of mathematicians in Alexandria who used the name Euclid, having derived it from Euclid of Megara. (O’Connor & Robertson, 1999) There exists a great deal of evidence suggesting that Euclid, whether that be an individual person or a team of mathematicians, founded a prestigious mathematics school in Alexandria.

The authors of the article, JJ O’Connor and EF Robertson, point out that while the third hypothesis is unlikely, we see the example of Bourbaki in the 20^th century. However, the members were renowned mathematicians in their own right. If “Euclid” was a secret team of competent mathematicians, we don’t know who they were.

I find the argument that Euclid led a team of mathematicians most convincing. I believe Euclid was a person because of the stories and history associated with the man, but I believe that the work he performed was too much for any one man to produce without a team behind him. The Elements became a textbook that was used for centuries after his death, and I just think it’s unlikely that a work that comprehensive is something that came from just one person.

Other pieces of evidence that lead me to believe in the idea that Euclid was an actual person was the different accounts of Euclid’s relationship with others, especially mathematicians. Pappus, known as “the last of the great Greek geometers”, (O’Connor & Roberton, Pappus of Alexandria, 1999) said that Euclid was “… most fair and well disposed towards all who were able in any measure to advance mathematics, careful in no way to give offence, and although an exact scholar not vaunting himself.” The fact that Pappus gave such a specific description makes it seem unlikely that Euclid was merely a creation of other mathematicians of that time period. One other story that the authors recounted was originally told by Stobaeus, who was a compiler of works from many ancient Greek authors (Wikipedia, 2014). He said, “…someone who had begun to learn geometry with Euclid, when he had learnt the first theorem, asked Euclid “What shall I get by learning these things?” Euclid called his slave and said “Give him three pence since he must make gain out of what he learns.” My favorite story, and one that I had actually heard before in several other circles, is that of the interaction between Euclid and Ptolemy. Proclus says, “they say that Ptolemy once asked him if there were a shorter way to study geometry than the Elements, to which he replied that there was no royal road to geometry.” I loved that. I’ve often heard that same phrase applied to other subjects, athletics, and religious pursuits. Indeed, there is no “royal road” to anything that is of worth.

The Elements, like we’ve discussed in class, is Euclid’s greatest claim to fame. In the article, Robertson and O’Connor quote Sir Thomas Heath, who was responsible for translating the works of many ancient Greek authors, including Euclid to English. Heath said, “This wonderful book, with all its imperfections, which are indeed slight enough when account is taken of the date it appeared, is and will doubtless remain the greatest mathematical textbook of all time. … Even in Greek times the most accomplished mathematicians occupied themselves with it: Heron, Pappus, Porphyry, Proclus and Simplicius wrote commentaries; Theon of Alexandria re-edited it, altering the language here and there, mostly with a view to greater clearness and consistency…” (O’Connor & Robertson, Euclid of Alexandria, 1999) Indeed, Euclid’s name will always be reverenced as one of the formative thinkers in all mathematics for his work on one of the greatest textbooks ever produced by men. However, I maintain my belief that The Elements was not the work of one man, but the work of many. I also believe that it should in no way detract from the respect and praise given to Euclid, the individual, as one of the greatest mathematicians of all time.

The Beauty of The Elements

A stone statue by Joseph Durham depicting the famous mathematician Euclid. Image: Garrett Coakley via flickr.

When I was in high school, I eventually learned about the mathematical subject known as geometry. Unlike most schools though, instead of our teacher having us sit down and listen to them talk about the subject, our teacher had each and every one of us go to the library and rent a copy of Euclid’s Elements (Book 1). From that point on till the end of the first semester, each day we would separately read from Euclid’s Elements and then try to prove to our teacher each and every postulate using Euclid’s methods. It wasn’t until recently that I discovered that most children do not learn about geometry in this fashion and how unique of an experience I had. While I can see some of the possible advantages behind the new ways people learn about geometry, I still believe that Euclid’s The Elements has its own advantages that some of these other sources don’t.

One of the most noticeable things about The Elements is that each and every one of Euclid’s postulates build exceptionally well off of each other. While I see proofs building off of each other in most other texts books, there is just something about the way it is done in The Elements that feels much smoother. Perhaps the big advantage with a book like The Elements is that it was never meant to be a “text” book but rather a book for people who are interested in learning about geometry. Because of this, it doesn’t have to continually throw out real world examples or ask the reader to try to use this proof in specific scenarios. Instead, The Elements will just make a statements, go about proving that statement, and then go straight into making another statement and most likely prove it using the previously proven statement.

Another difference between The Elements and other geometry books which I believe makes it far superior is the general way in which it goes about solving proofs. Nowadays, most geometry books will use a popular form of algebra and a number system to solve equations. However, Euclid’s Elements is fully self-contained and takes nothing for granted. Because this book was created in a time where people didn’t necessarily have access to other sources, everything that is necessary to understand what is being stated in this book is there; including its own algebraic system. This self-contained version of algebra within The Elements uses simple comparisons between lines and shapes to each other which replaces constants and variables found in other forms of algebra (which is also explained in the book) to prove that the different statements that are being made are true. These comparisons in combination with previously proven statements allows The Elements to create proofs of all different kinds. While the algebraic like system Euclid’s Elements uses to solve equations may be a little difficult to get one’s mind around sometimes it makes the proofs within its pages much more difficult to refute than other geometry books.

So, why do we not use this book to teach students about geometry today? Perhaps the biggest reason and most obvious is that The Elements is a difficult book to read. Unlike most textbooks today, it doesn’t use numbers and doesn’t give examples. However, just because current day geometry books are easier to teach with and easier for students to understand does not mean that they are better books. Perhaps the final reason that I believe The Elements is such a great geometry book compared to others is that the reader must want to learn about geometry if they wish to get anywhere in Euclid’s Elements.  But, if they are able to get through Euclid’s Elements, they will have a much stronger fundamental idea of geometry than from other textbooks. While it is easy to state the fact that someone who survives being stranded in the wilderness will have a better idea of how to survive in the wild than someone who hasn’t, it doesn’t change the fact that it is true.

Going back to my classroom experience, I thoroughly enjoyed going through the proofs in The Elements and I would spend most of my lunch time going to my teacher and proofing more of Euclid’s Statements. After about 2 weeks of starting the book, I had finished it. After that point, I spent the rest of time in class helping other students understand The Elements. Unfortunately, most of the other students had a hard time getting through that semester and only a few other students were able to understand it in a similar fashion as myself. However, those among us who did understand Euclid’s The Elements had no troubles passing the second semester of class which was going back to the more common form of geometry. In conclusion, I believe that Euclid’s Elements is a fantastic book that does more for geometry than any other book out there and, if someone is really interested in geometry, they should do their best to read through and understand The Elements if they want the best foundation in geometry they can have.

Sources:

(http://en.wikipedia.org/wiki/Euclid%27s_Elements)

(https://archive.org/details/bub_gb_UhgPAAAAIAAJ)

Illiterate Math or ∫ ? what? ≠ :)

In class the other day, a student wondered, “Why don’t they just use symbols? Didn’t Euclid or Eudoxus notice how much easier it would be to use symbols and pictures? All of this language is so difficult.”

I believe no one would deny that mathematics is its own language. In fact, I think most people would categorize modern mathematics as a very foreign language. Symbols, operations, variables, etc. are mashed together in such a way that only a mathematician can understand what it is expressed or being questioned. This is absolutely necessary on some level. Mathematicians, and other users of mathematics, need an efficient and effective way to represent operations and the language of computation. On the other hand, it is quite sad to me that a “universal” language is so foreign. Indeed, if mathematics is a universal language, why is it understood by so few, and even despised by so many?

Mathematics didn’t start out being a foreign language. As described in Boyer and Merzbach, the earliest algebra descriptions did not use symbols. It was referred to as rhetorical algebra and an equation like x+2-z=3 would be written similar to: a thing plus two and minus a thing is equal to three. Sure, this description seems a little weird and clunky, but for most people, I argue it is easier to figure out and less “scary” or off-putting than the typical symbolic equation given above.

In Book I, proposition 41 from Euclid’s Elements, it describes something in language that all people could attempt to understand.

Thus, if a parallelogram has the same base as a triangle, and is between the same parallels, then the parallelogram is double (the area) of the triangle.

The above sentence may be difficult to understand, but it is approachable by anyone. All of the words can be defined or looked up. Representing mathematics with words allows everyone to be mathematically literate. I believe the loss of language in mathematics is a hindrance to it accessibility, popularity, and literateness.

Why was Euclid’s Elements so popular? Everyone seems to have read it, from President’s to peasants, for at least 1000 years. Part of the reason for this may be that it was actually readable. Anyone who could read, could read Euclid’s Elements. It is hard to imagine my calculus text being written in such a way, but it is important to ask, is there value in writing it in that way? Would it be a worthwhile undertaking to attempt to translate mathematics into words? Would that make it more accessible, more enjoyable, and more relevant to everyone? Would non-mathematicians be able to pick up a book and attempt to understand it? I know very few people who could pick up this and understand it:

However, most people might understand or could at least attempt to understand: write out one-half, eight times. Between each one-half write a plus symbol. Now, starting at zero and continuing until seven, raise each iteration of one-half to a power. The first one-half is raised to zero and the last one-half is raised to 7. Compute each iteration, and then add it all together. This is called summing a sequence of numbers from zero to seven. If I read this description when I first saw the above notation, I would not have been so afraid of it. I also might have tried to do it. Instead, seeing this foreign language scared me off. It just seemed too complicated to understand and figure out.

Most of my favorite math books do just that (Zero: The Biography of a Dangerous Idea; 100 Essential Things you didn’t know you didn’t know). They are books about math that contain numerous verbal descriptions of operations, ideas, and calculations. Sure, they also contain real formulas, but that is a supplement to the written description of the idea. Finding ways to use language to write about and describe math is important. Math should be accessible to all even if it is not computable by all. Wouldn’t approaching math in this way allow people to be at least as literate in mathematics as they are in English?

The Thirteen Books of Euclid’s Elements; translated from the text of Heiberg with introduction and commentary by Sir Thomas L. Heath, K.C.B., K.C.V.O., F.R.S., SC.D. Camb., Hon. D.SC.
Oxford, Volume III, Books X-XIII and Appendix: https://archive.org/details/JL_Heiberg___EUCLIDS_ELEMENTS_OF_GEOMETRY

A History of Mathematics, Jan 11, 2011 by Carl B. Boyer and Uta C. Merzbach

equation taken from http://www.math.utah.edu/grad/exam/DiffEquatF2014.pdf