Modular Arithmetic and how it works

As children, we grew up learning how to count to 10. Why 10? Well this could be easily justified using the fact that we as humans have 10 fingers and any whole number up to 10 could be easily represented by a quick show of fingers. But what happened when we, as children with this new found power of counting objects up to 10, encountered a number greater than 10? Did we take off our shoes and start counting with our toes? That might have solved the issue for numbers greater than 10 but less than 20 (assuming you aren’t polydactylic) but in all reality, we needed a way to transcend the idea of representing objects with our fingers and/or toes and represent any number, no matter how large.

How did we do this? By using a Place Value system with a base 10. “Place Value” means that using a limited number of symbols, we can represent any number by using these symbols in a variety of combinations. The value of each symbol is based on the position or “place” where the symbol is located in the sequence of symbols.

For example, pick a base. The very first column or “place” should be used for all the symbols preceding the base until the base itself is reached. This is called the “units” place or informally as the “ones” place. This place is usually the farthest left or right place in a sequence. For instructional purposes and for familiarity, we will place the units place on the far right of the sequence.

Once the base has been reached, a second place will be added to the left indicating how many “bases” have been reached. When the amount of “bases reached” has reached the base amount, then a new place is added, again to the left, indicating how many bases of bases have been reached and so on and so forth.

For example, our familiar base 10 system works as follows:

_____ . . . _____ _____ _____ _____

A comma is added after every 3 digits for practical purposes to easily differentiate places in more complex combinations of numbers.

Now let’s go back 4,000 years ago to Sumer, a region of Mesopotamia, (modern-day Iraq). There, children learned to count, but using 60 as a base. Why 60? Did the children of that time have 60 fingers and/or toes? Probably not. The reason for using this number as a base has not been explicitly recorded but there are two convincing hypothesis on why a base 60 number system developed.

One idea, is that instead of using their whole finger to represent a single number, the Babylonians actually counted the 12 knuckles of the four fingers on one hand, using the thumb as a “pointer” and the five fingers on the other as multiples of twelve. So on one hand they had 1-12 and on the other they had how many 12’s, for a total of 12 x 5 = 60.

The other idea is that the number 60 has many divisors, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. In fact, 60 is the smallest number divisible by all integers from 1 to 6. This could prove very useful by being able to do division using more whole numbers and resulting in less fractions.

Base 60 is still used in many aspects of our lives today such as the 60 seconds in a minute and the 60 minutes in an hour. The circles is traditionally divided into which are also subdivided into 60 minutes of arc and further divided into 60 seconds of arc.

Modular Arithmetic

Image: Spindled, via Wikimedia Commons.

Now that we have a brief overview about bases, we can apply the power of Modular Arithmetic to change counting bases. Modular Arithmetic is a very handy and useful tool in mathematics invented by the famous Mathematician Carl Friedrich Gauss in 1801. We know that the number line is infinitely long but if we were to wrap this infinitely long number line around a circle of a given circumference n, we would notice that numbers would “line up” or over lap around the circle. This is the idea behind modular arithmetic. Keep in mind that we are dealing with integers here and not the real numbers.

So the number indicating how large the circle is n, is called the modulus. And we say that after one wrap around, any numbers that line up are congruent. In mathematical terms, when a number a, leaves the same remainder as a number b, we say a and b are congruent written

a ≡ b mod n

The “mod n” part is just notation letting us know that we are in mod n and is not actually part of the equation, per se. However, when the context is understood, it should be OK to omit writing this every time.

In general, any modulo n has n residue classes, one for each integer from 0 to n-1.

Let’s use the timer on your microwave as an example of a base. So we will have n residue classes from the integers 0 to 59.

0, 1, 2, 3, … 56, 57, 58 59

We call this modulo 60 or mod 60 for short. When we add 1 to 59, we return to 0. This is true for any modulus, even our own familiar base 10 (when we add 1 to 9, we return to 0) or even every day objects like traffic lights (Red, Green, Yellow, Red, …). The integers from 0 to 59 in our base 60 example are called Residue Classes.

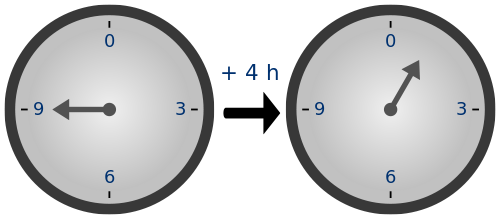
Now for a quick example, when I was in the military, we would tell time using the 24-hour clock. This is different than the usual 12 hour clock where all 24 hours are represented twice and distinguished using A.M. or P.M.

So when I would get asked what time I would be ready to get picked on Friday for the weekend, I would reply 1600. Of course this did not make sense to most people because the face of a clock only has the numbers 1-12 listed on it. How could I explain correctly to them what time to pick me up so as to maximize our time together on the sunny beaches of San Diego? Using modular arithmetic of course!

Numbers are said to be congruent if their difference is divisible by the modulus. Or stated more succinctly, a is congruent to b if a-b is divisible by n shown algebraically

a ≡ b mod n if a-b / kn for some k

This basically means that the difference must be divisible by the base.

In our example, let’s show that 1600 is congruent to 4:00. For lingo purposes, just think of the colon as “hundred hours” to be in step with 1600. 1600 – 400 is 1200, a multiple of 12. Written

1600 ≡ 400 mod 1200

1600-400 /1200

“So 4:00 P.M. civilian. Don’t be late.”

Another cool example of things you can do with modular arithmetic is calculate the last digit or remainder of a huge number like . Try doing that by hand! Here is how we would do it mod 10.

19¹⁹ ≡ 9¹⁹; (because 19 is congruent to 9 mod 10)

(9²)⁹*9 ≡ (81)⁹*9 ;

(1)⁹*9 ≡ 9; (because 81 is congruent to 1 mod 10)

References:

Use of base 60 using hands

https://www.youtube.com/watch?v=_XBJBG3vKS8&list=PLMpRfUAf1yQGhrBCe6moyrW49mJlNgf0n

Base 60 as a base

http://www.storyofmathematics.com/sumerian.html

Sub-divisions of angles into minutes and seconds

http://en.wikipedia.org/wiki/Minute_of_arc

Modular Arithmetic

http://en.wikipedia.org/wiki/Modular_arithmetic

https://brilliant.org/discussions/thread/modular-arithmetic-2/

We Need more Fingers

Image: Sun Ladder, via Wikimedia Commons.

Our base ten number system is so ingrained in us that it is difficult to imagine using anything else.  With our ten fingers to count on, it makes sense that we have ten symbols to represent numbers.  Despite this, other cultures have used extremely different number systems.  The Ancient Mesopotamians used a sexigesimal, or base 60, number system.  The Mayans used a vigesimal, or base 20 system.  Roman numerals are used to number the Rocky movies despite them being almost completely useless.  Most computer techies are familiar with binary and hexadecimal.  Many early peoples even used a system with only 5 symbols (Boyer 3).  Our current number system may be intuitive but it may not be the best one around.  What if we had an extra finger on each hand?  We would be using a much more useful number system.  We should move away from the decimal numbers we currently use, and switch to a base twelve, or dozenal, number system.

There are several reasons to seek more mainstream use of base 12.  The factors of a number, or the numbers that divide into it evenly, determine a lot about the number.  Twelve can be broken down into more factors than ten can be.  Ten is divisible by only 2 and 5, whereas 12 is divisible by 2, 3, 4, and 6.  This gives 12 an advantage over 10.  The additional factors make it easier to think of many fractions, such as fourths and sixths, since they will now have only have a single significant digit after the point.  This is particularly effective when dividing 1 into thirds because it will not leave us with an infinite series of 3s like it does in decimal.  The simple tricks that help us do arithmetic, such as the fact that in base ten if a number ends in an even number the whole number is even and thus is divisible by 2, depend on the factors that make up our number base.  Since 12 has more factors, similar tricks can be used for more numbers.  In base twelve, if a number ends in 0, 4, or 8 the entire number is divisible by 4, if it ends in a 0, 3, 6, or 9 then it is divisible by 3.  We will not even miss out on the trick for evens that base ten has since twelve is also divisible by 2.  The trick we now currently use for 11, where you alternate adding and subtracting the digits of a number and see if the resulting number is divisible by 11, will work for 13 when we make the switch, because now 13 will be the number that is one larger than our base.  Don’t be concerned about 11, because we will have a new trick for 11 in dozenal.  The trick we currently use for 9, where we just add up the digits of a number and then check if the sum is divisible by 9, will work with 11 once we change to dozenal.  It is easy to check the divisibility of far more numbers in dozenal than it is to check in decimal.

For a dozenal system, we would have to make some changes to the actual symbols we use.  We have 10 symbols to use for the numbers 0-9 and a base twelve number system would need 2 more symbols to represent ten and eleven.  There are many different sets of symbols we can use to fill the two new places.  Some number sets use *, and # to represent ten and eleven in order to correspond to the symbols on most phone number pads.  Others use X, and a backwards 3, and some use a backwards and upside down 2 and 3.  Some sets completely replace all the symbols we use for 0-9, along with adding two new symbols.  We could use any group of numbers that would help us acclimate to a base twelve system.

Some things that we already do everyday would assist in our transfer to a base twelve system.  We already have specific terminology for 12 and several of its powers.  We use the word dozen to refer to twelve, a gross for a dozen dozens, or twelve sets of twelve, and a great gross for a dozen gross, or twelve gross.  When looking at a clock, we already deal with twelves to determine the time.  Figuring out what the time is 5 hours after 10 pm is basically the same thing as adding 5 to 10 in base twelve.  As Professor James Monroe notes, thinking of egg cartons makes thinking of dozenal numbers easy.  If 1 egg carton holds 12 eggs, and 1 case holds twelve cartons, a number like 426 in base 12 can simply be thought of as 4 cases, 2 cartons, and 6 loose eggs.  Twelves seem almost as prominent in daily life as the number ten.

Despite the familiarity we already have with base twelve, switching to dozenal will still be incredibly difficult.  Because we would have more digits, kids would have to memorize larger multiplication tables.  Luckily, the tables will not be anywhere near as large as they would be if we still used Cuneiform.  However, the real difficulty in switching has little to do with what number base we want to use.  The trouble will be in converting all the numbers on everything that we use.  Every road sign, price tag, page number, and countless other places have numbers that will need to be converted to base twelve.  This will be more difficult than changing from using imperial units to metric units, and America still has not completely converted to metric.  Here in the U.S., some things are measured with metric units, but we still measure distances in miles and a sack of potatoes at the grocery store is measured in pounds.  Also, to add more difficulty, in metric we would have to come up with new prefixes that are based on powers of 12 instead of powers of 10.  Changing to dozenal numbers is such a monumental task we may not be able to accomplish it.

In spite of the difficulties, I believe we should do it.  The conversion will not happen overnight.  We must look further down the road.  Perhaps, start by teaching people how to do arithmetic in dozenal in addition to teaching them the usual decimal system that we use.  Then when people are comfortable with it, we could move on to using base twelve alongside decimal.  Eventually, our ancestors will be able to move on to a better number system than what we currently have.  Like the Kwisatz Haderach from Frank Herbert’s Dune, we must endure temporary struggles in order to achieve the Golden Path.

Source

Boyer, Carl B., and Uta C. Merzbach. A History of Mathematics. 3rd ed. Hoboken, NJ: Jon Wiley and Sons, 2010. Print.

Additional Material

http://www.dozenal.org/drupal/

http://www.dozenalsociety.org.uk/

http://youtu.be/U6xJfP7-HCc