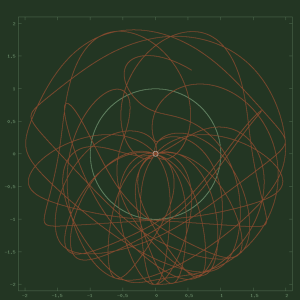
Chaos is the science of surprises, of the nonlinear and the unpredictable. It teaches us to expect the unexpected. Chaos Theory is the branch of mathematics that deals with complex systems whose behavior is highly sensitive to slight changes in conditions, so that small alterations can give rise to strikingly great consequences. This is what makes Chaos theory so interesting, the thought that a butterfly flapping its wings has a real connection with a cloud floating thousands of miles away.
This is called the Butterfly effect. The butterfly effect occurs under two conditions: When the system is nonlinear and when each state of the system is determined by the previous state. In other words, the output at each moment is repeatedly entered back into the system for another cycle through the mathematical functions that determine the system. Here is an example to help explain non-linearity and its connection to the Butterfly effect: “Let us take the air itself. We will assume that it is at a constant temperature and pressure and comprises atoms that collide elastically (no energy lost as heat). For how long could we predict the trajectories of the molecules (given an ideal computer)? The answer is almost no time at all, a few collisions only, a tiny fraction of a second. The system is nonlinear, as are all real systems.” (Calresco)
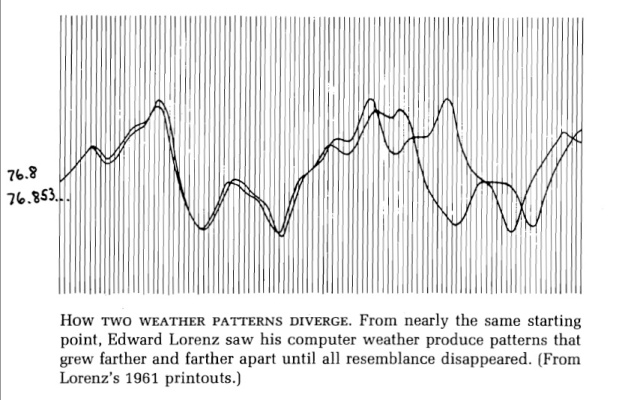
The two main components of chaos theory are the ideas that systems – no matter how complex they may be – rely upon an underlying order, and that very simple or small systems and events can cause very complex behaviors or events. This latter idea is known as sensitive dependence on initial conditions, a circumstance discovered by Edward Lorenz (who is generally credited as the first experimenter in the area of chaos) in the early 1960s. Complex systems are very difficult to model because it is nearly impossible to know all the initial conditions perfectly. This causes issues in predicting the final result of the complex system, one small error would be amplified dramatically.
An example of the Chaos theory in a real world settings is the stock market. This is known as a chaotic system due to feedback. As the value of a stock rises or falls, people are inclined to buy or sell that stock. This in turn further affects the price of the stock, causing a chaotic rise or fall. Another example is the double rod pendulum experiment. For this experiment you take a rod with a free flowing bend half way down, it is then dropped from any point. If you trace the bottom of the rod or have it ‘draw’ where it has been you get a graphical trajectory. Now you start the pendulum from a slightly different initial position and let it swing freely yet again. This results in a completely different graphical trajectory as the first time the experiment was conducted. The double rod pendulum is one of the simplest dynamical systems that has chaotic solutions.
If you think of every human on earth as a billiard ball, the interaction of two ‘colliding’ causes a chain of collisions that effect you. Each and every person just existing has some reaction with all the others. As a PhD math professor mentioned in his work on ‘Major open problems in chaos theory and nonlinear dynamics’. “Overall, chaos is understood but not tamed. In fact, it is not clear whether or not it is tractable! More specifically, the mechanism of how chaotic dynamics operates is understood; how to effectively describe chaos in term of some sort of averaging (chaos engineering) is beyond reach.”(Li)
Image sources:
http://commons.wikimedia.org/wiki/File:Butterfly%27s_effect..jpg
http://commons.wikimedia.org/wiki/File:Doublependulumpath.png
Sources:
Li: http://arxiv.org/pdf/1305.2864.pdf
http://www.calresco.org/nonlin.htm
http://fractalfoundation.org/resources/what-is-chaos-theory/
http://whatis.techtarget.com/definition/chaos-theory