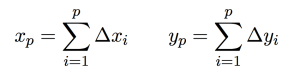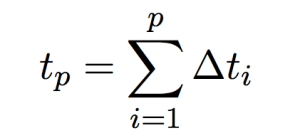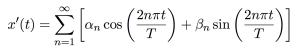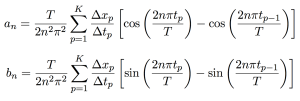G.H. Hardy and Genetic Equilibrium

Who knew that an unlikely friendship and a few games of cricket with one of the greatest mathematicians in the early 20th Century could lead to a breakthrough in population genetics?

Today, it is almost commonplace for us in the scientific community to accept the influence natural selection and Mendelian genetics have on one another, however for the majority of human history this was not the case. Up until the early 1900s, many scientists believed that these concepts were nothing more than two opposing and unassociated positions on heredity. Scientists were torn between a theory of inheritance (a.k.a. Mendelian genetics) and a theory of evolution through natural selection. Although natural selection could account for variation, which inheritance could not, it offered no real explanation on how traits were passed on to the next generation. For the most part, scientists could not see how well Mendel’s theory of inheritance worked with Darwin’s theory of evolution because they did not have a way to quantify the relationship. It was not until the introduction of the theorem of genetic equilibrium that biologists acquired the necessary mathematical rigor to show how inheritance and natural selection interacted. One of the men who helped provide this framework was G.H. Hardy.

G. H. Hardy. Image: public domain, via Wikimedia Commons.

Godfrey Harold (G.H.) Hardy was a renowned English mathematician who lived between 1877-1947 and is best known for his accomplishments in number theory and for his work with the another great mathematician, Srinivasa Ramanujan. For a man who was such an outspoken supporter of pure mathematics and abhorred any practical application of his work[5], it is ironic that he should have such a powerful influence on a field of applied mathematics and help shape our very understanding of population genetics.

How did a pure mathematician come to work on population genetics? Well it all started with a few games of cricket. Whilst teaching at the University of Cambridge, Hardy would often interact with professors in other departments through friendly games of cricket and evening common meals [1]. It was through these interactions that Hardy came to know Reginald Punnett, cofounder of the genetics department at Cambridge and developer of Punnett Squares, which are named for him, and developed a close friendship with him[13].

Punnett, being one of the foremost experts in population genetics, was in the thick of the debate over inheritance vs. evolution. His interactions with contemporaries like G. Udny Yule, made him wonder why a population’s genotype, or the genes found in each person, did not eventually contain only variations, known as alleles, of a particular gene that are dominant. This was the question he posed to Hardy in 1908, and Hardy’s response was nigh on brilliant. The answer was so simple that it almost seemed obvious. Hardy even expressed that “I should have expected the very simple point which I wish to make to have been familiar to biologists’’ [4]. His solution was so simple in fact that unbeknownst to him, another scientist had reached the same conclusion around the same time in Germany [17]. In time, this concept would be known as Hardy-Weinberg Equilibrium (HWE).

In short, HWE asserts that when a population is not experiencing any genetic changes that would cause it to evolve, such as genetic drift, gene flow, selective mating, etc., then the allele (a_f) and genotypic frequencies (g_f) will remain constant within a given population (P’). To calculate the g_f for humans, a diploid species that receives two complete sets of chromosomes from their parents, we simply look at the proportion of genotypes in P’.

0 < g_f < 1

To calculate the a_f, we look at the case where either the gene variation is homozygous and contains two copies of the alleles (dominant—AA || recessive—aa) or heterozygous and only has one copy of each allele (Aa). P’ achieves “equilibrium” when these frequencies do not change.

Hardy’s proof of these constant frequencies for humans, a diploid species that receives two complete sets of chromosomes from its parents, is as follows[1][4]:

If parental genotypic proportions are p AA: 2q Aa: r aa, then the offspring’s would be (p + q)²: 2(p + q)(q + r): (q + r)². With four equations (the three genotype frequencies and p + 2q + r = 1) and three unknowns, there must be a relation among them. ‘‘It is easy to see that . . . this is q² = pr” 

Which is then broken down as:

q =(p + q)(q + r) = q(p + r) + pr + q²

Then to:

q² = q(1- p – r) – pr = 2q² – pr     ——->   q² = pr

In order to fully account for the population, the g_f and a_f must sum to 1. And, since each subsequent generation will have the same number of genes, the frequencies remain constant and follows either a binomial or multinomial distribution.

One important thing to keep in mind, however, is that almost every population is experiencing some form of evolutionary change. So, while HWE shows that the frequencies don’t change or disappear, it is best used as a baseline model to test for changes or equilibrium.

When using the Hardy-Weinberg theorem to test for equilibrium, researchers divide the genotypic expressions into two homozygous events: HHο and hhο. The union of each event’s frequency ( f ), is then calculated to give the estimated number of alleles (N_f). In this case, the expression for HWE could read something like this:

N_f = f(HHο) ∪ f(hhο)

However, another way to view this expression is to represent the frequency of each homozygous event as single variable, i.e. p and q. Using p to represent the frequency of one dominant homozygous event (H) and q to represent the frequency of one recessive homozygous event (h), gives the following: p = f(H) and q = f(h). It then follows that p² = f(HHο) and q² = f(hhο). By using the Rule of Addition and Associative Property to calculate the union of the two event’s frequencies, we are left with F = (p+q)². Given that the genotype frequencies must sum to one, the prevailing expression for HWE emerges when F is expanded:

F = p² +2pq + q² = 1

Using this formula, researchers can create a baseline model of P’ and then identify evolutionary pressures by comparing any subsequent frequencies of alleles and genotypes (F∝) to F. The data can then be visually represented as a change of allele frequency with respect to time.

HWE represents the curious situation that populations experience when their allele frequencies change. This situation is realized by first assuming complete dominance, then calculating the frequency of alleles, and then using the resultant number as a baseline with which to compare any subsequent values. Although there are some limitations on how we can use HWE—namely, identifying complete dominance, the model is very useful in identifying any evolutionary pressures a population may be experiencing and is one of the most important principles in population genetics. Developed, in part, by G.H. Hardy, it connected two key theories: the theory of inheritance and the theory of evolution. Although, mathematically speaking, his observation/discovery was almost trivial, Hardy provided the mathematical rigor the field sorely needed in order to see that the genotypes didn’t completely disappear and, in turn, forever changed the way we view the fields of biology and genetics.

Sources:

1. Edwards, A. W. F. “GH Hardy (1908) and Hardy–Weinberg Equilibrium.”Genetics3 (2008): 1143-1150.
2. Edwards, Anthony WF. Foundations of mathematical genetics. Cambridge University Press, 2000.
3. Guo, Sun Wei, and Elizabeth A. Thompson. “Performing the exact test of Hardy-Weinberg proportion for multiple alleles.” Biometrics(1992): 361-372.
4. Hardy, Godfrey H. “Mendelian proportions in a mixed population.” Science706 (1908): 49-50.
5. Hardy, G. H., & Snow, C. P. (1967). A mathematician’s apology. Reprinted, with a foreword by CP Snow. Cambridge University Press.
6. Pearson, Karl. “Mathematical contributions to the theory of evolution. XI. On the influence of natural selection on the variability and correlation of organs.”Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character(1903): 1-66.
7. Pearson, K., 1904. Mathematical contributions to the theory of evolution. XII. On a generalised theory of alternative inheritance, with special reference to Mendel’s laws. Philos. Trans. R. Soc. A 203 53–86.
8. Punnett, R. C., 1908. Mendelism in relation to disease. Proc. R. Soc. Med. 1 135–168.[PMC free article] [PubMed]
9. Punnett, R. C., 1911. Mendelism. Macmillan, London.
10. Punnett, R. C., 1915. Mimicry in Butterflies. Cambridge University Press, Cambridge/London/New York.
11. Punnett, R. C., 1917. Eliminating feeblemindedness. J. Hered. 8 464–465.
12. Punnett, R. C., 1950. Early days of genetics. Heredity 4 1–10.
13. Snow, C. P., 1967. G. H. Hardy. Macmillan, London.
14. Stern, C., 1943. The Hardy–Weinberg law. Science 97 137–138. [PubMed]
15. Sturtevant, A. H., 1965. A History of Genetics. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
16. Weinberg, Wilhelm. “Über vererbungsgesetze beim menschen.” Molecular and General Genetics MGG1 (1908): 440-460.
17. Weinberg, W. “On the demonstration of heredity in man.” Boyer SH, trans (1963) Papers on human genetics. Prentice Hall, Englewood Cliffs, NJ(1908).

Figure: Wikimedia Commons

Rise and Fall of Wasan

Since most would not be able to read my report on Sangaku (Artfully done tablet of Geometry) I thought I would do a blog post on the rise and fall of wasan (Japanese Mathematics) for you all to enjoy. Never mind it’s a topic I know a lot about now and have done a bunch of research on the topic.

The Japanese didn’t really have their unique math until about the year 1627 when Jink ̄o-ki was published. This was the first Japanese mathematics book published. The Jink ̄o-ki was a Japanese publication that explained how to use the soroban (Japanese name for the abacus) to do things like calculate pi, and would provide other math instruction and problems. Until then, much of the learning and study in math came from the classics of China, with heavy emphasis on The Nine Chapters and Cheng’s Treatise. I’ll explain a bit as to why there was such a long delay in developing mathematics.

Leading up to the late 1500s, most uses for math in Japan was to levy taxes on the land and for basic arithmetic for business transactions. The government of the time actually created The Department of Arithmetic Intelligence to go to each landowner and measure the property so the owner would know how much tax to pay.

These math specialists only knew just enough geometry to get the area of the land and calculate the tax required. The government saw math as a means to an end for acquiring money. This meant that math was a tool used by the government and only a special few were educated in mathematics as deemed necessary. But since there was no one to teach them, they had to rely on the Nine Chapters to be their teacher.

Around the early 1600s things began to change. A new set of rulers named the Tokugawa family took over all of Japan, uniting all the land under one government. Taxes were no longer tied to the amount of land owned and The Department of Arithmetic Intelligence was no more. This, in turn, led the farmers to no longer know how much land they had and, as consequence, the amount of food they could produce.

The Tokugawas also brought about another important change, the closing of the Japanese boarder. Iemitsu Tokugawa outlawed Christianity and closed the boarders. The problem was that a growing number of converts started a community together and began to band together. At the same time the Spaniards attempted to compete for converts and in a bold attempt to be the only missionaries in Japan told the Tokugawa family that the other nation’s missionaries were trying to create an army to conquer Japan. The Spaniards’ plan backfired and all missionaries were put to death along with those that would not give up on Christianity.

With the closing of the boarders and all the enemies of the government crushed, a period of peace was created called the Edo period in Japan that lasted until 1868 when boarders were opened again. It was during this period that the Japanese culture became its own and flourished. Everything from haiku poems to flower arranging to tea ceremonies was created during this time. By the end of the Edo period a gentleman was expected to know “medicine, poetry, the tea ceremony, music, the hand drum, the noh dance, etiquette, the appreciation of craft work, arithmetic and calculation . . . not to mention literary composition, reading and writing.” (Hidetoshi)

During the time of Great Peace the samurai became the new noble men of Japan. No longer needed as warriors, many were given government jobs to help ease them into normal lives. As consequence, the men became some of the more educated citizens. That being said, the pay they received for working for the government was terrible. Most samurai had to pick up 2^nd jobs; many of them become traveling schoolteachers.

The stage was now ripe for an explosion of learning. We had farmers that needed to learn math, we had samurai that needed second jobs, and a place for it all to happen, the local shrine or Buddhist temple. Since there were no school buildings, most lessons happened at the shrines and temples that dotted the land. This encouraged more people to gather together for religious, educational, social functions. Over the next century the Japanese people would have the highest literacy rate of all the nations and become one of the most educated.

During this time, the people began to make sangaku, which is basically an artistically made wooden tablet containing a geometric problem and most of the time the solution. These tablets would adorn the temples and shrines showing off the newest knowledge learned. However, these tablets also had a deeper meaning. These sangaku became a way of thanking the gods and spirits for the new knowledge.

Many of the sangaku that have been found focused on finding lengths, areas of various shapes, and even volumes. The sangaku found below is one example of finding a length. The problem asks to find the diameter of the north circle inside of the fan. The problem is setup so that the entire area of the fan is a third of a circle and you can assume you know the diameter of the south circle. The answer ends up being (sqrt(3072) + 62 )/193 times the diameter of the south circle.

Sadly, wasan (Japanese Mathematics) was one of the few things that didn’t survive the Japanese Renaissance, which is why many of the records of wasan and sangaku are only now being discovered. At the end of the Edo period a new government was formed that outlaws wasan from being taught. It turns out that wasan lacked Calculus but more importantly, was different than the rest of the world. With the opening of the boarders, the government needed to adopt Western Mathematics to be able to communicate with all the new trade partners that were being re-established. To that end, a law was created that outlawed wasan and Western math was forced in the schools. Anyone that still taught wasan had his teaching license stripped and imprisoned.

Reference:

Hidetoshi, F., & Rothman, T. (2008). Sacred Mathematics. Princeton, New Jersey: Princeton University Press.

What Does Being Correct Mean?

In class, we were discussing the Parallel Postulate by Euclid. Basically it says that if you draw a straight line on top of two other lines so that they intersect, and if the angles on the same side of the first line are less than 2 right angles (180^o), the two lines will intersect at some point on the same side.

Image: 6054, via Wikimedia Commons.

It’s weird learning about proving something that feels so elementary that I assumed it was just true by definition. I mean I can just look at the picture and it certainly looks like it should be correct just by careful inspection. But I guess that doesn’t really prove it without a shadow of doubt. What if what I was looking at was 179.999^o and I just said they would never touch even though they would intersect given enough space. Granted, I would assume it was 180^o so I would be correct based on the assumption being true.

When I look at this problem, I can’t help but reflect on the lessons, experiences, and “truths” that have instilled within me from previous mentors and teachers. It becomes very hard to try and think about other approaches or ideas other than “duh that true”.

What allowed me to think about this Postulate was learning about how other people through out history thought about the Parallel Postulate and created their own “new math”; their own pseudogeometry; their own imaginary geometry. Here I am unable to think “outside the lines”, but these other people created whole new systems from looking at the problem from a different angle. I have no problems creating weird parallels with my jokes and puns but can’t seem to do the same thing with math. (Yes, I love bad puns).

Poincare and Lobachevski were both people that worked in this pseudogeometry, which is now called hyperbolic geometry. (The former or “normal” geometry is considered “Euclidean Geometry”). In hyperbolic geometry it’s possible to have lines that would normally intersect in Euclidian space be considered parallel and non-intersecting in hyperbolic space. I think looking at the picture below will really help. I know it wasn’t until I built a hyperbolic plane by hand that it really sunk in for me. ( Make your own at http://www.math.tamu.edu/~frank.sottile/research/subject/stories/hyperbolic_football/index.html )

A hyperbolic triangle. Public domain, via Wikimedia Commons.

Reflecting on the on hyperbolic plane I began to try to remember a time when what the instructor was teaching conflicted with something I already knew. As I thought I remembered something an art teacher told me about vanishing points. So imagine you’re standing on some railroad tracks that stretch straight forward for miles. As you look down the tracks, as you would if you were actually a train, at some point the individual components would become one whole line. Instead of seeing the left rail, the right rail, and everything else you would see a railroad track. At that point, the left and right rails have effectively become one, unable to tell them apart. Now what would happen if a train went down those rails that look like they became one? The train becomes smaller, or at least, it looks like the train is shrinking. At the time I could only think about how the teacher lost her mind. It wasn’t until I looked down a straight road that I realized how right she was.

After thinking about how perspective is everything I began to wonder what other things are different than they appear? I asked a friend, and she mentioned she actually had to unlearn some thing to be able to Fence (as in the sport) correctly. She told me that she had to change the way she extended her arm in order to be able to obtain the longest reach possible.

It turns out that a straight line with your arm is not the best way to have the longest reach. In all my learning, I had been taught that you to get the longest linear distance with line segments are to put each line segment end to end along the same axis. But in fencing, doing just that with your arm is not the longest. Why is fencing different?

When hold the sword in your hand, it seems that your muscles tighten to hold the load and your arm up. By tightening your muscles, you shorten your reach by as much as 2 inches for some people. When your muscles are relaxed, the joints can loosen allowing more space between the bones, which lengthens your arm. So by relaxing your arm a bit so it’s not parallel with the ground, your sword can reach just a little bit further.

Is math wrong when it comes to the physics of people and fencing? Absolutely not! In my case, it’s the model that the math was used on that was wrong. I assumed the arm was a rigid object with hinges at the shoulder, elbow, and wrist. Since I had modeled the arm in this fashion any math done to the model would never take into account the possibility of expansion of the hinges. Assumptions are the downfall of many people.

Proof of the Pythagorean theorem

History of the Pythagorean theorem

The Pythagorean theorem is one of the greatest scientific discovery of the human, and it is also one of the basic elementary geometry theorems. There are also many other names to call this theorem, like Shang-Gao theorem, Bai-Niu theorem and so on. Someone maybe will ask that what is the Pythagorean theorem. According to Wikipedia, the Pythagorean theorem “is a relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.[1]” This theorem has a very long history. Almost all ancient civilizations (Greece, China, Egypt, Babylon, India, etc.) have studied this theorem. In the West, this theorem was called Pythagorean theorem. According to legend, Pythagoras, an ancient Greek mathematician and philosopher, was the first person to discover this theorem in 550 BC. Unfortunately Pythagoras’ method of proving this theorem had been lost and we could not see how he proved now. But another famous Greek mathematician, Euclid (330 BC – 275 BC), gave us a good proof in his book called Euclid’s Elements. But Pythagoras was not the first person who discovered this theorem around the world. Ancient China discovered this theorem much earlier than him. So there is another name for the Pythagorean theorem in China, the Gou-Gu theorem. Zhong Jing is the first book about mathematics in China. And in the beginning of this book, there was a conversation between Zhong Gong and Shang Gao. They were talking about the way to solve the triangle problem. From this conversation, we could know that they already found out the Pythagorean theorem around 1100 BC. They found this theorem 500 years earlier than Pythagorean.

Proof of the Pythagorean theorem

Usually in a right triangle, we need to find the length of the third side when we already know the length of other two sides. For such problems, we can directly use the formula to calculate. In many problems, we need this theorem to solve many complex questions. And then, I will introduce two basic method to prove the Pythagorean theorem.

1) Proof by Zhao Shuang

In China, Zhang Shuang was the first person who gave us the earliest proof of the Pythagorean theorem. Zhao Shuang created a picture of “Pythagorean Round Square”, and used method of symbolic-graphic combination gave us a detailed proof of the Pythagorean theorem.

Assume a, b are two Right-angle side (b > a) and c is Hypotenuse. Then each area of a right triangle is equal to ab/2.

[Fig.1] Proof by Zhao Shuang

∵ RtΔDAH ≌ RtΔABE,

∴ ∠HDA = ∠EAB.

∵ ∠HAD + ∠HAD = 90º,

∴ ∠EAB + ∠HAD = 90º,

∴ ABCD is a square with side c, and the area of ABCD is equal to c².

∵ EF = FG =GH =HE = DG―DH , ∠HEF = 90º.

∴ EFGH is also a square, and the area of ABCD is equal to (b-a)².

∴ 4 *(1/2)(DG*DH)+(DG-DH)²=AD²

∴ DH²+DG²=AD²

2) Proof by Euclid

Just like we said before, Euclid gave us a good proof in his Euclid’s Elements. He also used method of symbolic-graphic combination.

In the first, we draw three squares and the side of each square are a, b, c. And then, let points H、C、B in a straight line. Next we draw two lines between F、B and C、D and draw a line parallel to BD and CE from A. This line will perpendicularly intersect BC and DE at K and L.

[Fig.2] Proof by Euclid

∵ BF = BA，BC = BD,

∠FBC = ∠ABD,

∴ ΔFBC ≌ ΔABD

∵ The area of ΔFBC is equal to (1/2)*FG² and the area of ΔABD is half of the area of BDLK.

∴ The area of BDLK is equal to FG². And then we can find the area of KLCE is equal to AH² with the same method.

∵ The area of BDEC = The area of BDLK + The area of KLCE.

∴ FG²+AH²=BD²

Conclusion

The Pythagorean theorem’s development has exerted a significant impact on mathematics. And this theorem gave us an idea to solve geometric problems with Algebraic thinking. It is also a great example about symbolic-graphic combination. This idea is very important for solving mathematical problems. By the Pythagorean theorem, we can derive a number of other true propositions and theorems, which will greatly facilitate our understanding of geometry problems, but it also has driven the development of mathematics.

Reference

[1] http://en.wikipedia.org/wiki/Pythagorean_theorem

[Fig.1] https://upload.wikimedia.org/wikipedia/commons/e/e0/ZhaoShuangRtTriangleGraph.PNG

[Fig.2]https://upload.wikimedia.org/wikipedia/commons/5/59/Illustration_to_Euclid%27s_proof_of_the_Pythagorean_theorem2.svg

Differential & Integral Calculus – The Math of Change

Most will remember their first experience with calculus. From limits to derivatives, rates of changes, and integrals, it was as if the heavens had opened up and the beauty of mathematics was finally made clear. There was, in fact, more to the world than routine numerical manipulation. Numbers and symbols became the foundational building blocks with which theories could be written down, examined, and shared with others. The language of mathematics was emerging and with it a new realm of thinking. For me, calculus marked the beginning of an intellectual awakening and with it a new way of thinking. It is therefore perhaps worthy to examine the early development of our modern calculus and to provide a more concrete historical context.

The method of exhaustion. Image: Margaret Nelson, illustration for New York Times article “Take it to the Limit” by Steven Strogatz.

The distinguishing feature of our modern calculus is, undoubtedly, its unique ability to utilize the power of infinitesimals. However, this power was only realized after more than a millennium of intense mathematical debate and reformation. To the early Greek mathematicians, the notion of infinity was but a paradoxical concept lacking the geometric backing necessary to put it on a rigorous footing. It was this initial struggle to provide both a convincing and proper proof for the existence and usage of infinitesimals that led to some of the greatest mathematical development this world has ever seen. The necessity for this development is believed to be the result of early attempts to calculate difficult volumes and areas of various objects. Among the first advancements was the use of the method of exhaustion. First used by the Greek mathematician Eudoxus (c. 408-355 BC) and later refined by the Chinese mathematician Liu Hui in the 3^rd century AD^[1], the method of exhaustion was initially used as a means of “sandwiching” a desired value between two known values through repeated application of a given procedure. A notable application of this method was its use in estimating the true value of pi through inscribing/circumscribing a circle with higher degree n-gons.^[1] With the age of Archimedes (c. 287-212) came the development of heuristics – a practical mathematical methodology not guaranteed to be optimal or perfect, but sufficient for the immediate goals.^[2] Followed by advancements made by Indian mathematicians on trigonometric functions and summations (specifically work on integration), the groundwork for modern limiting analysis began to unfold and thus the relevance for infinitesimals in the mathematical world.

Isaac Newton. Image: Portrait of Isaac Newton by Sir Godfrey Kneller. Public domain.

By the turn of the 17^th century, many influential mathematicians including Isaac Barrow, René Descartes, Pierre de Fermat, Blaise Pascal, John Wallis, and others had already been applying the results on infinitesimals to the study of tangent lines and differentiation.^[2] However, when we think of modern calculus today the first names to come to mind are almost certainly Isaac Newton and Gottfried Leibniz. Before 1650, much of Europe was still in what historians refer to as the Hellenistic age of mathematics. Prior to the contributions of Newton and Leibniz, European mathematics was largely an “informal mass of various techniques, methods, notations, and theories.”^[2] Through the creation of a more structured and algorithmic approach to mathematics, Newton and Leibniz succeeded in transforming the heart of the mathematical system itself giving rise to what we now call “the calculus.”

Both Newton and Leibniz shared the belief that the tangent could be defined as a ratio but Newton insisted that it was simply the ratio between ordinates and abscissas (the x and y coordinates respectively in the plane in regular Euclidean geometry).^[2] Newton further added that the integral was merely the “sum of the ordinates for infinitesimals intervals in the abscissa” (i.e., the sum of an infinite number of rectangles).^[4] From Leibniz we gain the well-known “Leibniz notation” still in use today. Leibniz denoted infinitesimal increments of abscissas and ordinates as dx and dy and the sum of infinitely many infinitesimally thin rectangles as a “long s” which today constitutes our modern integral symbol ò.^[2] To Leibniz, the world was a collection of infinitesimal points and that infinitesimals were ideal quantities “less than any given quantity.”^[3] Here we might draw the connection between this description and our modern use of the greek letter e (epsilon) – a fundamental tool in modern analysis in which assertions can be made by proving that a desired property is true provided we can always produce a value less than any given (usually small) epsilon.

From Newton, on the other hand, we get the groundwork for differential calculus which he developed through his theory on Fluxionary Calculus first published in his work Methodus Fluxionum.^[2] Initially bothered by the use of infinitesimals in his calculations, Newton saught to avoid using them by instead forming calculations based on ratios of changes. He defined the rate of generated change as a fluxion (represented by a dotted letter) and the quantity generated as a fluent. He went on to define the derivative as the “ultimate ratio of change,” which he considered to be the ratio between evanescent increments (the ratio of fluxions) exactly at the moment in question – does this sound familiar to the instanteous rate of change? Newton is credited with saying that “the ultimate ratio is the ratio as the increments vanish into nothingness.”^[2/3] The word “vanish” best reflects the idea of a value approaching zero in a limit.

The derivative of a function.

Contrary to popular belief, Newton and Leibniz did not develop the same calculus nor did they conceive of our modern Calculus. Both aimed to create a system in which one could easily manage variable quantities but their intial approaches varied. Newton believed change was a variable quantity over time while for Leibniz change was the difference ranging over a sequence of infinitely close values.^[3] The historical debate has therefore been, who invented calculus first? The current understanding is that Newton began work on what he called “the science of fluents and fluxions” no later than 1666. Leibniz on the other hand did not begin work until 1673. Between 1673 and 1677, there exists documented correspondence between Leibniz and several English scientists (as well as Newton himself) where it is believed that he may have come into contact with some of Newton’s   unpublished manuscripts.^[2] However, there is no clear consensus on how heavily this may have actually influenced Leibniz’s work. Eventually both Newton and Leibniz became personally involved in the matter and in 1711 began to formally accuse each other of plagiarism.^[2/3] Then in the 1820’s, following the efforts of the Analytical society, Leibnizian analytical calculus was formally accepted in England.^[2] Today, both Newton and Leibniz are credited for independently developing the foundations of calculus but it is Leibniz who is credited with giving the discipline the name it has today: “calculus.”

The applications of differential and integral calculus are far reaching and cannot be overstated. From modern physics to neoclassical economics, there is hardly a discipline that does not rely on the tools of calculus. Over the course of thousands of years of mathematical development and countless instrumental players (e.g. Newton and Leibniz), we now have at our disposal some of the most advanced and beautifully simple problem solving tools the world has ever seen. What will be the next breakthrough? The next calculus? Only time will tell. What is certain is that the future of mathematics is, indeed, very bright.

Works Cited

^[1]Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). “A comparison of Archimdes’ and Liu Hui’s studies of circles”. Chinese studies in the history and philosophy of science and technology 130. Springer. p. 279. ISBN 0-7923-3463-9., Chapter , p. 279

^[2]“History of Calculus.” Wikipedia. Wikimedia Foundation, n.d. Web. 14 Mar. 2015.

^[3]“A History of the Calculus.” Calculus History. N.p., n.d. Web. 14 Mar. 2015.

^[4] Valentine, Vincent. “Editor’s Corner: Voltaire and The Man Who Knew Too Much, Que Sera, Sera, by Vincent Valentine.” Editor’s Corner: Voltaire and The Man Who Knew Too Much, Que Sera, Sera, by Vincent Valentine. ISHLT, Sept. 2014. Web. 15 Apr. 2015.

Elliptic Fourier Descriptors

Elliptic Fourier Descriptors (EFDs) are one really good answer to the question: How can I mathematically describe a close contour?

That’s nice, but why would we want to do this?

One good reason, with apologies to Randall Munroe, is that after reading xkcd #26 you probably really wanted to take the Fourier transform of your cat. You and me both! Below, we’ll do exactly that, using the method described by Kuhl and Giardina (1982) in their paper ‘Elliptic Fourier Descriptors with Chain Encodings’.

Image: xkcd by Randall Munroe

Of course this isn’t exactly fair- you’ve already taken the Fourier transform of your cat if you’ve ever saved a picture of it as a jpg or listened to it meow over the phone (listen, I don’t know what you do with your free time, but I’m not here to judge) because Fourier transforms are really popular in both video and audio compression.

Step One: Image Pre-Processing

I’m actually a dog person, so I found my creative-commons licensed cat photo through flickr. To make preprocessing easier, I was looking for a monotone cat that was entirely in the frame.

First I extracted the cat from the background using Preview’s great cropping tool. You could automate this segmentation with a script, but for one image it’s easier to do it by hand.

Next I created a binary version of the segmented image with the Matlab one-liner: imwrite(im2bw(imread(‘cat.png’)), ‘bw_cat.png’). The image is binary because every pixel is either pure black or pure white. This binary image can be thought of as a matrix where every pixel makes up one matrix entry and is either 0 (white) or 1 (black).

Original image: Emiliyan Dikanarov, via Flickr.

Step Two: Extracting the Boundary

Now that we have our binary image let’s grab our contour. At this step we’ll represent the contour as a list of the (x,y) positions of the pixels that make up the boundary of the cat.

From our preprocessing step we assured that all non-zero (white) pixels belonged to our cat, so we can just walk through each column of our matrix until we find the first non-zero entry. This pixel must be on the boundary of the cat! From there, we can just walk around the contour by following neighboring boundary pixels until we’ve found every pixel in the contour. At this point we’ll have a list of (x, y) positions of all the boundary pixels.

But wait!

I claimed that Elliptic Fourier Descriptors were a way to mathematically describe a close contour- why isn’t this description, a list of the (x,y) coordinates of all the pixels in the contour good enough of a mathematical description?

I lied when I motivated EFDs as a great way to take a Fourier transform of your cat.

The real use-case for EFDs is creating features for machine learning algorithms; something like teaching a computer to classify photos of cats from non-cats. What we really need is some way to saying how ‘cat-like’ an object in a photo looks- and that’s why this mathematical representation falls short. This representation isn’t position or scale invariant, and is really susceptible to noise- this means that if I have a more zoomed out photo of the same cat in a different position in the frame or it’s a bit blurry, then my algorithm won’t stand a chance of realizing it’s still a cat.

We’ll see below that all these problems are resolved when we take the Fourier transform.

But first, to make taking the Fourier transform easier, we’ll change out of a coordinate encoding. Instead, we’ll use a Freeman chain encoding, which describes each point in a shape relative to each previous point.

Step Three: Freeman Chain Encodings

A Freeman chain encoding is a piece-wise linear approximation of a continuous curve. Each segment of the continuous curve is approximated by one of eight line segments, denoted by a₀ – a₇ in the graph below. The line segments with even index have unit length, and the odd line segments with odd with odd index have a length of √2. This will be convenient later on!

For our purposes, we’re encoding a contour in a digital image, which is already a discrete approximation of a continuous curve. Below on the left is an example of the type of curve we might want to approximate; the chart on the right shows its Freeman chain encoding.

Detour: Fourier Series

In general, a Fourier series is a way to approximate a periodic function. A periodic function is just a waveform, and a Fourier transform breaks complex waveforms into sums of simple ones.

We can also use Fourier series to approximate non-periodic functions so long as we specify an interval. Below I’ll show an example of how we can approximate x² on [-pi, pi]; we do this by setting the “period” of x² to be [-pi, pi]. We pretend that the part of the non-periodic function we want to approximate is periodic outside of the interval we’re considering it over.

The really beautiful thing about this approximation is that we can make it arbitrarily good, that is, we can make the error between the approximation and the real function as small as we want.

The Fourier series f(x) is described by the equation below- we see that the Fourier series is parameterized entirely by its constituent a_n’s and b_n’s.

This approximation approximates the true function arbitrarily well on any finite interval. If we instead replace the infinite sum with a finite one, from n = 1 to k, this is called the k’th harmonic; the higher the value of k, the better the approximation.

Let’s look at a few harmonics of x² on [-pi, pi]. The graphs below were generated in WolframAlpha with the command “overlay[{plot FourierSeries[x^2, x, k], plot x^2}]” with k replaced by the number of the harmonic we want to look at (ie, 1, 2, 3).

Notice that the function of the harmonic is written in blue in the legend of the graph. It’s amazing how fast we converge to a good approximation!

Click to embiggen.

 

Step Four: Fourier Transform and Time Derivative

Okay, back to what we were doing with our cat.

Ask not what you can do for your Fourier series, but what your Fourier series can do for you.

Now that we have the Freeman chain encoding of our cat contour, and are convinced that Fourier series are the way of the future, let’s look at what they can do for us. Below is a really quick explanation of the Kuhl-Giardina 1982 paper.

Our first goal is to find how we can compute those coefficients we talked about in the previous section, an and bn.

First we’ll notice that we can take separate our chain encoding into its x and y projections. We’ll define x_p and y_p, the projection of the first p links in our chain encoding to be the sum of the differences between all the previous links.

Notice that it’s the exact same story in both the x and y direction, so for ease we’ll just work the x version out below and understand that exactly the same logic will hold for y.

We’ll consider the time derivative of x. When we say “time” here we actually mean the length of the chain, for instance, the “time” contribution of any horizontal or vertical link is 1, and the contribution of any diagonal link is √2. The “time” of the p’th link is just the sum of all the times of the previous links.

The punchline is going to be that we’ll write this derivative in two different ways- one way which we can compute from the chain code, and one way which will involve the coefficients we’re trying to find a_n and b_n. Then we can solve for a_n and b_n.

Time derivative: First Form!

Here ‘n’ is which harmonic we’re on, T is the period (the interval we’re looking at the function on) and alpha_n and beta_n depend on the slope of each line segment.

This is very good news, because we can compute everything in this form of the time derivative! Because we’re using a Freeman chain encoding (just piecewise linear segments) the slope of any line segment is either 0, (plus/minus) 1, or (plus/minus) √2.

Time derivative: Second Form!

This is also good for us, because this form includes the coefficients we’re trying to solve for. Solving for a_n and b_n we get:

We know how to compute a_n and b_n! T is the period (the interval), n is the number of the harmonic that we’re looking at, p is the index of the chain link, K is the total number of chain links, (del x_p/del t_p) is the slope of each link, and t_p and t_p-1 are the lengths of the chain at the p’th link.

The exact same thing happens in the y direction, so we call the a_n value in the y direction c_n and the b_n value in the y direction d_n.

Step Five: Elliptic Equation

Phew! We figured out how to find all our coefficients. How’s this going to help us with our cat?

We’ll use these coefficients to modify an ellipse- after all, we basically want a modified ellipse to approximate our closed contour.

Below is the equation that gives the n’th Elliptic Fourier Descriptor.

Notice that this looks a lot like the equation for an ellipse; the xy term comes in so that we can rotate the ellipse.

Another good thing about these coefficients is that they’re the same regardless of how the contour is rotated, what size it is, or where in the frame of the image it is.

Now we’ve got the cat in the bag.

Step Six: Results!

Using the description we found above, we’ll approximate the cat contour that we found. The true contour is given in blue, and the approximation is given in red.

Notice that with 10 harmonics we already have a pretty good approximation, but with 70 harmonics we can fit much finer features.

For real-world applications, like creating features for machine learning, fitting fine features might be not be desirable, because you might be over-fitting to random noise instead your data.

10 harmonics on the left, 20 in the middle, and 70 on the right.

I also decided this was a great opportunity to find the EFD of Randall Munroe.
I grabbed another creative commons image, and found the 70th harmonic of Randall Munroe.

Appendix: Matlab code

Here’s the code you need to replicate everything we did.

Segment the image
imwrite(im2bw(imread(‘cat.png’)), ‘bw_cat.png’)
Generate the chain code
chain = mk_chain(bw_cat.png’);
[cc] = chaincode(chain);

You’ll need to grab mk_chain.m off of this website first.
Really all it does is make a call to the Matlab function bwtraceboundary
Also be warned that this code often failed for me, if this happens for you just replace the <dir> on the last line (line 36) with <‘SE’>.

Generate the EFD
chain = mk_chain(bw_cat.png’);
[cc] = chaincode(chain);
coeffs = calc_harmonic_coefficients(transpose([cc.code]), 70)

First you’ll need to grab all the m files off of this website.

You can replace 70 with whatever number of harmonic you want to look at. Coeffs will be a matrix with 4 numbers, these are the coefficients a₇₀, b₇₀, c₇₀, d₇₀.

See what your chain code looks like
chain = mk_chain(bw_cat.png’);
[cc] = chaincode(chain);
figure
plot_chain_code(transpose([cc.code]));

See what your EFD looks like compared to your chain code
chain = mk_chain(bw_cat.png’);
[cc] = chaincode(chain);
figure
plot_chain_code(transpose([cc.code]));
hold
plot_fourier_approx(transpose([cc.code]), 70, 50, 0, ‘r’);

Again, you can replace 70 with however many harmonics you’d like to see.

Chinese Mathematics: Not so Different from Western Mathematics

When we talk about mathematical discoveries certain names are mentioned.  These are names like Pascal, Euclid, Fermat, and Euler. These people become our mathematician Heroes. In our eyes, we often believe they pioneered the study. When we hear names like Mo Jing and Yang Hui in western society, most of us probably don’t even think anything of them.

But did you know that many of the great mathematical discoveries made in Western Mathematics were also made by Chinese mathematicians? In fact some mathematical discoveries we attribute to western mathematicians were even made by Chinese mathematicians far before they were discovered in the west.

I bring this up not necessarily to shame western culture, but because I find it fascinating.  We have two cultures that really didn’t intermix ideas and traditions, yet it seems that they have made many similar mathematical discoveries. In my opinion these similarities in a way show that two totally different cultures with cast differences still have profound similarities that can unite them.

Also in the great debate of whether math is manmade or discovered I personally believe the similarity between western and Chinese mathematics is a point for Team Discovered.  That might be only because I currently am on Team Discovered, though. I believe this is a point for Team Discovered because I feel if two separate cultures that are not trading ideas come up with the same mathematical truths then maybe they discovered them instead of just happened to share the same inventive thoughts. Still maybe this is the exact reason I should join Team Invention and I am just not thinking through my argument all the way.

Let’s talk about some of the similar discoveries in Chinese mathematics and western mathematics.  Let’s try to focus on the person behind a concept that both cultures discover/invented.  If feasible we should mention when the discovery/invention came about and how. Also how did it influence mathematics and the human race? I won’t focus on it, but you might even want to see if what we discuss puts you on team invention or team discovery for mathematics.

I guess the first Chinese work that I would like to point out is more of a compilation of Chinese works than the work of one individual, but did you know that of book very much like Euclid’s Elements existed in China?  This book was the canon of a group of people called Mo Jing. They were the followers of Mozi and the canon contained, among philosophical insights, works on geometry. Mozi was actually a Chinese philosopher, but his teachings inspired his followers to consider mathematics as well. In fact this book contained a definition for a point similar to Euclid’s. To be specific, “a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it.” (http://history.cultural-china.com/en/167H8715H13206.html)

Now, one of the most famous mathematical discoveries is “Pascal’s Triangle.” “Pascal’s Triangle,” is a fascinating work. To describe it you build it from the top down.  Put a one at the top.  Build the triangle down adding 1 more number in each row. The value of the number below is the sum of the two numbers directly above it. If it is an edge case the number is 1.

Image: Drini and Conrad.Irwin, via Wikimedia Commons.

This discovery, made by Pascal while, through letters, he was exploring probability with Fermat, was also discovered much earlier by a Chinese man named Yang Hui. Even before Yang Hui it was described earlier by Jia Xian in 1100.  Yang Hui in his book attributes the triangle to Jia and acknowledged that it was through this triangle that he found square roots as well as cubed roots.

I feel it is also very important that we discuss the book Zhou Bi Suan Jing.  This book, which is a collection of anonymous works, contains one of the first proofs of the well-known and widely used Pythagorean Theorem. As a refresher, this a²+b²=c².  Controversy overshadows the actual date of the book which is assumed to be around 1046-256 BCE.

We can clearly see that mathematical ideas are not monopolized by western tradition.  In fact, in my studies of Chinese mathematics, I found references Pascal’s Triangle being found in India and Iran. Pascal was a genius, but clearly he was not the original discoverer of the triangle that bears his name. Mathematics is a global study, applied in many ways similarly by many cultures.

Take some time and identify a culture.  Make sure it is a culture that is so different from your own that, in a history class, this culture would study completely different things than what you studied. Now take what you know of your culture and the culture you chose and find similarities. Sometimes this can be hard. There are similarities such as in many cultures families eat together, but there are also many differences. What I am saying here is that in many ways math can be one of those similarities. This is neat! Math is as much a western study as it is an eastern study.

So next time you are learning about a western mathematician and how awesome he/she is, take some time and ask yourself if maybe the same ideas were explored by someone else in a different time in a different part of the world. Maybe even look it up. You might be surprised by what you find.

http://www.astro.umd.edu/~peel/CPSP118D_101/content/Zhou_bi_suan_jing.pdf

http://www-history.mcs.st-and.ac.uk/Biographies/Yang_Hui.html

http://history.cultural-china.com/en/167H8715H13206.html

What are the p-adic numbers?

The p-adic numbers are a completion of rational numbers with respect to the p-adic norm and form a non-Archimedean field. They stand in contrast to the real numbers, which are a completion of the rationals with respect to absolute value and which do respect the Archimedean property. The p-adic numbers were first described in 1987 by Kurt Hensel and later generalized in the early 20^th century by József Kürschák which paved the way for a myriad of mathematical work involving the P-adics in the just over a century since.

To start talking about the p-adics it makes sense to start with the Archimedean property, which as mentioned above the p-adics do not adhere to.  First we need an absolute value function or valuation, ||, which is basically a function that gives some concept of magnitude to an element of a field (so it’s a mapping from a field to the positive real numbers). Given this, the zero element should map to zero and the valuation of the product of two elements should be the same as the product of the valuation of each element individually. The last condition (which determines whether or not the valuation is Archimedean) is that if the norm of an element is less than or equal to 1, then the norm of 1 plus that element is less than some constant, C, which is independent of the choice of x. If the last condition holds for C equal to 1, then the valuation satisfies the ultrametric inequality: the valuation of 2 elements is less than or equal to the maximum of the valuation of each element. If the ultrametric inequality is satisfied then the valuation is non-Archimedean. Otherwise it is an Archimedean valuation.

While this is a bit opaque, it makes more sense now moving into defining Archimedean fields: a field is Archimedean if given a field with an associated valuation and a non-zero element, x, of that field, then there exists some natural number n such that |Σ_k=1ⁿx|>1. Otherwise,  the field is non-Archimedean and the ultrametric inequality holds. Basically what this means is that if we can measure distance and we are living in a nice Archimedean world, if we walk forward we can go as far as we want. While if we were to live in a non-Archimedean world and we try to walk forward we would at best stay in place and possibly move backward.

Now that that’s out of the way and (hopefully) the weirdness of a non-Archimedean world has been established, it’s time to talk about the p-adics. Any non-zero rational number, x, may be expressed in the form x ,where a and b are relatively prime to some fixed prime p and r is an integer. Using this, the p-adic norm of x is defined as |x|=p^-r , which is non-Archimedean. For example, when p=3, |6|=|2*3|=1/3, |9|=|3²|=1/9 and |6+9|=|15|=|3*5|=1/3 or when p=5 , |4/75|=|4/(5²*3)|= 25, |13/250|=|13/(2*5³)|=125 while |4/75 + 13/250|=|17/325|=|17/(5²*13)|=25. So now that we have this we can proceed identically as when constructing the real numbers using the absolute value and define Q­_p as the set of equivalence classes of Cauchy sequences with respect the p-adic norm. After some work it can be shown that every element in Q­_pcan be written uniquely as Σ_k=ma_kp^k,where a_m does not equal zero and m may be any integer.

The most common use of p-adics I found was in showing the existence (or lack thereof) of rational or integer solutions to problems. For example, the Hasse principle (also known as the local-global prinicipal ) was discovered by Helmut Hasse in the 1920’s and attempts to give a partial converse of the statement that if a polynomial of the form Σa_ijxⁱy^j+Σb_ixⁱ+c=0 has a rational solution then it has a solution for all expansions of Q. The Hasse principal asserts that if such a polynomial has a solution in R and every Q_p then it has solution in Q. An example of this is x²-2=0, which has (irrational) solution square root of 2 in R. However, it does not have solution in Q₅ , and so by the Hasse principal it does not have a solution in Q, which we know to be true. Another use of the P-adics which is fairly interesting is in transferring standard real or complex polynomial equations to their tropical (the semi ring of the reals with the addition of an infinity element under the laws of composition addition and min (or max)) polynomial counterpart, a process which runs into issues due to the necessity of the ultrametric inequality.

Sources:

http://www.cut-the-knot.org/blue/LocalGlobal.shtml

http://en.wikipedia.org/wiki/P-adic_number

http://mathworld.wolfram.com/p-adicNumber.html

http://mathworld.wolfram.com/p-adicNorm.html

http://mathworld.wolfram.com/Valuation.html

http://www1.spms.ntu.edu.sg/~frederique/antchap5.pdf

Click to access HasseMinkowski.pdf

Isaac Newton and his Contributions to Mathematics

Sir Isaac Newton. Image: Arthur Shuster & Arthur E. Shipley, via Wikimedia Commons..

In class we discussed the Fundamental Theorem of Calculus and how Isaac Newton contributed to it, but what other discoveries did he make?

Sir Isacc Newton was born on January 4, 1643, but in England they used the Julian Calender at that time and his birthday was on Christmas Day 1642. He was born in Woolsthorpe-by-Colsterworth, a hamlet in the county of Lincolnshire. His father had already passed prior to his birth and his mother remarried after his birth and left Isaac to live with her mother. He went to The King’s School, Grantham from the time he was twelve until he was seventeen. His mother removed him from school after the death of her second husband, but later allowed him to return by the encouragement of the school’s headmaster. He rose to be at the top in rankings in his school, mainly motivated to get revenge towards a bully. He began attending Trinity College in Cambridge in 1661. After receiving his degree he developed his theories on calculus over the span of two years during the plague [1].

Newton’s work in calculus intitially started as a way to find the slope at any point on a curve whose slope was constantly varying (the slope of a tangent line to the curve at any point). He calculated the derivative in order to find the slope. He called this the “method of fluxions” rather than differentiation. That is because he termed “fluxion” as the instantaneous rate of change at a point on the curve and “fluents” as the changing values of x and y. He then established that the opposite of differentiation is integration, which he called the “method of fluents”. This allowed him to create the First Fundamental Theorem of Calculus, which states that if a function is integrated and then differentiated the original function can be obtained because differentiation and integration are inverse functions [2].

Controversy later arose over who developed calculus. Newton didn’t publish anything about calculus until 1693, but German mathematician Leibniz published his own version of the theory in 1684. The Royal Society accused Leibniz of plagiarism in 1699 and the dispute caused a scandal to occur in 1711 when the Royal Society claimed Newton was the real discoverer of calculus. The scandal got worse when it was discovered that the accusations against Leibniz were actually written by Newton. The dispute between Newton and Leibniz went on until the death of Leibniz. It is now believed that both developed the theories of Calculus independently, both with very different notations. It should also be noted that Newton actually developed his Fundamental Theory of Calculus between 1665 and 1667, but waited to publish his works due to fear of being criticized and causing controversy [1].

Newton not only discovered calculus but he is also credited for the discovery of the generalised binomial theorem. This theorem describes the algebraic expansion of powers of a binomial. He also contributed to the theory of finite differences, he used fractional exponents and coordinate geometry to get solutions to Diophantine equations, he developed a method for finding better approximation to the zeroes or roots of a function, and he was the first to use infinite power series.

His work and discoveries were not limited to mathematics; he also developed theories in optics and gravitation. He observed that prisms refract different colors at different angles, which led him to conclude that color is a property intrinsic to light. He developed his theory of color by noting that regardless if colored light was reflected, scattered, or transmitted it remained the same color. Therefore color is the result of objects interacting with colored light and objects do not generate their own colors themselves [1].

Sir Isaac Newton was a truly amazing mathematician and scientist. He achieved so much in his lifetime and the amount of discoveries he made can seem almost impossible. He helped make huge advancements in mathematics and created theorems that we still use heavily to this day.

[1] http://en.wikipedia.org/wiki/Isaac_Newton

[2] http://www.storyofmathematics.com/17th_newton.html

Leonardo of Pisa – The Great Fibonacci

Figure 1-Fibonacci. Image: Public domain, via Wikimedia Commons.

Most mathematically inclined people are familiar with the famous and unique Fibonacci sequence. Defined by the recurrence relation (*) F_n=F_n-1+F_n-2 with initial values F₁=1 and F₂=1 and (or sometimes F₀=1 and F₁=1), the Fibonacci sequence is an integer sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …) with many remarkable mathematical and real world applications. However, it seems that few are as well informed on the man behind this sequence as they are on the sequence itself. Did you know that Fibonacci didn’t even discover the sequence? Of course not! Predating Fibonacci by almost a century, the so called “Fibonacci sequence” was actually the brainchild of Indian mathematicians interested in poetic forms and meter who, through studying the unique arithmetic properties of certain linguistic sequences and syllable counts, derived a great deal of insight into some of the most fascinating mathematical patterns known today. But with a little bit of time (few hundred years), some historical distortion, inaccurate accreditation[1], and a healthy dose of blind western ethnocentrism and voila! Every high school kid in America now thinks there is a connection between Fibonacci and pizza. Or is it Pisa? (That’s a pun, laugh.) While often given more credit than deserved for the “discovery” of the sequence, Fibonacci was nonetheless an instrumental player in the development of arithmetic sequences, the spread of emerging new ideas, and in the advancement of mathematics as a whole. We thus postpone discussion of Fibonacci’s sequence – don’t worry, we shall return – to examine some of the other significant and often overlooked contributions of the “greatest European mathematician of the middle ages.”^[1]

Born around the year 1175 in Pisa, Italy, Leonardo of Pisa (more commonly known as Fibonacci) would have been 840 years old this year! (Can you guess the two indexing numbers between which Fibonacci’s age falls?[2]) The son of a customs officer, Fibonacci was raised in a North African education system under the influence of the Moors.[3] Fibonacci’s fortunate upbringing and educational experience allowed him the opportunity to visit many different places along the Mediterranean coast. It is during these travels that historians believe Fibonacci may have first developed an interest in mathematics and at some point come into contact with alternative arithmetic systems. Among these was the Hindu-Arabic number system – the positional number system most commonly used in mathematics today. It appears that we owe a great deal of respect to Fibonacci for, prior to introducing the Hindu-Arabic system to Europe, the predominant number system relied on the far more cumbersome use of roman numerals. It is interesting to note that while the Hindu-Arabic system may have been introduced to Europe as early as the 10^th century in the book Codex Vigilanus, it was Fibonacci who, in conjunction with the invention of printing in 1482, helped to gain support for the new system. In his book Liber abbaci[4], Fibonacci explains how arithmetic operations (i.e., addition, subtraction, multiplication, and division) are to be carried out and the advantages that come with the adoption of such a system.

Figure 2-Golden spiral. Image: Weisstein, Eric W. “Golden Spiral.” From MathWorld–A Wolfram Web Resource.

Whereas the number system most familiar to us uses the relative position of numbers next to each other to represent variable quantities (i.e., the 1’s, 10’s, 100’s, 1000’s, … place), Roman numerals rely on a set of standard measurement symbols which, in combination with others, can be used to express any desired quantity. The obvious problem with this approach is that it severely limits the numbers that can be reasonably represented by the given set of symbols. For example, the concise representation of the number four hundred seventy eight in the Hindu-Arabic system is simply 478 in which “4” is in the hundreds place, “7” is in the tens place, and “8” is in the ones place. In the Roman numeral system, however, this same number takes on the form CDLXXVIII. As numbers increase arbitrarily so does the complexity of their Roman numeral representation. The adoption of the Hindu-Arabic number system was, in large part, the result of Fibonacci’s publications and public support for this new way of thinking. Can you imagine trying to do modern mathematical analysis with numbers as clunky as MMMDCCXXXVIII??? Me either. Thanks, Fibonacci!

Fibonacci’s other works include publications on surveying techniques, area and volume measurement, Diophantine equations, commercial bookkeeping, and various contributions to geometry.^[4] But among these works nothing stands out more than that of Fibonacci’s sequence – yes, we have returned! Among the more interesting mathematical properties of Fibonacci’s sequence is undoubtedly its connection to the golden ratio (shall be defined shortly). To illustrate, we look momentarily at the ratios of several successive Fibonacci numbers. Beginning with F₁=1 and F₂=1 we see that the ratio F₂/F₁=1. Continuing in this manner using the recurrence relation (*) from above or any suitable Fibonacci table we find that F₃/F₂=2, F₄/F₃=3/2, F₅/F₄=5/3,F₆/F₅=8/5, F₇/F₆=13/8, F₈/F₇=21/13, … As the indexing number tends to infinity, the ratio of successive terms converge to the value 1.6180339887… (the golden ratio) denoted by the Greek letter phi. We may thus concisely represent this convergent value by the expression as the lim n–> infinity (F_n+1/F_n). Studied extensively, the golden ratio is a special value appearing in many areas of mathematics and in everyday life. Intimately connected to the concept of proportion, the golden ratio (sometimes called the golden proportion) is often viewed as the optimal aesthetic proportion of measurable quantities making it an important feature in fields including architecture, finance, geometry, and music. Perhaps surprisingly, the golden ratio has even been documented in nature with pine cones, shells, trees, ferns, crystal structures, and more all appearing to have physical properties related to the value of (e.g., the arrangement of branches around the stems of certain plants seem to follow the Fibonacci pattern). While an interesting number no doubt, we must not forget that mathematics is the business of patterns and all too often we draw conclusions and make big picture claims that are less supported by evidence and facts than we may believe. There is, in fact, a lot of “woo” behind the golden ratio and the informed reader is encouraged to be weary of unsubstantiated claims and grandiose connections to the universe. It is also worth mentioning that, using relatively basic linear algebra techniques, it is possible to derive a closed-form solution of the n-th Fibonacci number.

Figure 3-Computing the 18th Fibonacci Number in Mathematica.

Omitting the details (see link for thorough derivation), the n-th Fibonacci number may be computed directly using the formula F_n=((φ)⁽ⁿ⁺¹⁾+((-1)^(n-1)/(φ)^^(n-1))/((φ²)+1).^[5] While initially clunky in appearance, this formula is incredibly useful in determining any desired Fibonacci number as a function of the indexing value n. For example, the 18-th Fibonacci number may be calculated using F₁₈=((φ)⁽¹⁸⁺¹⁾+((-1)^(18-1)/(φ)^^(18-1))/((φ²)+1)=2584. Comparing this value to a list of Fibonacci numbers and to a Mathematica calculation (see picture above), we see that the 18-th Fibonacci number is, indeed, 2584. Without having to determine all previous numbers in the sequence, the above formula allows us to calculate directly any desired value in the sequence saving substantial amounts of time and processing power.

From the study of syllables and poetic forms in 12^th-century India to a closed-form solution for the n-th Fibonacci number via modern linear algebra techniques, our understanding of sequences and the important mathematical properties they possess is continuing to grow. Future study may reveal even greater mathematical truths whose applications we cannot yet conceive. It is thus the beauty of mathematics and the excitement of discovery that push us onward, compel us to dig deeper, and to learn more from the world we inhabit. Who knows, you might even be the next Leonardo of Pizza – errrrr Pisa. What patterns will you find?
[1] French mathematician Edouard Lucas (1842-1891) was the first to attribute Fibonacci’s name to the sequence. After which point little is ever mentioned of the Indian mathematicians who laid the groundwork for Fibonacci’s research.

[2] Answer: n=15 –> 610 and n=16 –> 987.

[3] Medieval Muslim inhabitants of the Maghreb, Iberian Peninsula, Sicily, and Malta.^[2]

[4] Translation: Book of Calculation^[3]

Bibliography

 ^[1] Knott, Ron. Who Was Fibonacci? N.p., 11 Mar. 1998. Web. 27 Apr. 2015.

^[2] “Moors.” Wikipedia. Wikimedia Foundation, n.d. Web. 27 Apr. 2015.

^[3] Leonardo Pisano – page 3: “Contributions to number theory”. Encyclopædia Britannica Online, 2006. Retrieved 18 September 2006.

^[4] “Famous Mathematicians.” The Greatest Mathematicians of All Time. N.p., n.d. Web. 28 Apr. 2015.

 ^[5] Grinfeld, Pavel. “Linear Algebra 18e: The Eigenvalue Decomposition and Fibonacci Numbers.” YouTube. YouTube, 2 Dec. 2014. Web. 28 Apr. 2015.

 Figure 1: Fibonacci. Digital image. Wikimedia Foundation, n.d. Web. 27 Apr. 2015.

Figure 2: Golden Spiral. Digital image. Mathworld. Wolfram, n.d. Web. 1 May 2015.

Figure 3: Ross, Andrew Q. Closed-Form Computation of Fibonacci. Digital image. Mathematica, 28 Apr. 2015. Web. 28 Apr. 2015.