Proof of the Pythagorean theorem

History of the Pythagorean theorem

The Pythagorean theorem is one of the greatest scientific discovery of the human, and it is also one of the basic elementary geometry theorems. There are also many other names to call this theorem, like Shang-Gao theorem, Bai-Niu theorem and so on. Someone maybe will ask that what is the Pythagorean theorem. According to Wikipedia, the Pythagorean theorem “is a relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.[1]” This theorem has a very long history. Almost all ancient civilizations (Greece, China, Egypt, Babylon, India, etc.) have studied this theorem. In the West, this theorem was called Pythagorean theorem. According to legend, Pythagoras, an ancient Greek mathematician and philosopher, was the first person to discover this theorem in 550 BC. Unfortunately Pythagoras’ method of proving this theorem had been lost and we could not see how he proved now. But another famous Greek mathematician, Euclid (330 BC – 275 BC), gave us a good proof in his book called Euclid’s Elements. But Pythagoras was not the first person who discovered this theorem around the world. Ancient China discovered this theorem much earlier than him. So there is another name for the Pythagorean theorem in China, the Gou-Gu theorem. Zhong Jing is the first book about mathematics in China. And in the beginning of this book, there was a conversation between Zhong Gong and Shang Gao. They were talking about the way to solve the triangle problem. From this conversation, we could know that they already found out the Pythagorean theorem around 1100 BC. They found this theorem 500 years earlier than Pythagorean.

Proof of the Pythagorean theorem

Usually in a right triangle, we need to find the length of the third side when we already know the length of other two sides. For such problems, we can directly use the formula to calculate. In many problems, we need this theorem to solve many complex questions. And then, I will introduce two basic method to prove the Pythagorean theorem.

1) Proof by Zhao Shuang

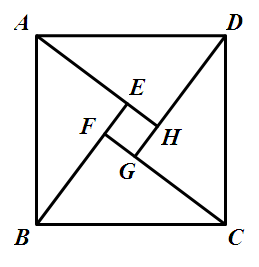
In China, Zhang Shuang was the first person who gave us the earliest proof of the Pythagorean theorem. Zhao Shuang created a picture of “Pythagorean Round Square”, and used method of symbolic-graphic combination gave us a detailed proof of the Pythagorean theorem.

Assume a, b are two Right-angle side (b > a) and c is Hypotenuse. Then each area of a right triangle is equal to ab/2.

[Fig.1] Proof by Zhao Shuang

∵ RtΔDAH ≌ RtΔABE,

∴ ∠HDA = ∠EAB.

∵ ∠HAD + ∠HAD = 90º,

∴ ∠EAB + ∠HAD = 90º,

∴ ABCD is a square with side c, and the area of ABCD is equal to c².

∵ EF = FG =GH =HE = DG―DH , ∠HEF = 90º.

∴ EFGH is also a square, and the area of ABCD is equal to (b-a)².

∴ 4 *(1/2)(DG*DH)+(DG-DH)²=AD²

∴ DH²+DG²=AD²

2) Proof by Euclid

Just like we said before, Euclid gave us a good proof in his Euclid’s Elements. He also used method of symbolic-graphic combination.

In the first, we draw three squares and the side of each square are a, b, c. And then, let points H、C、B in a straight line. Next we draw two lines between F、B and C、D and draw a line parallel to BD and CE from A. This line will perpendicularly intersect BC and DE at K and L.

[Fig.2] Proof by Euclid

∵ BF = BA，BC = BD,

∠FBC = ∠ABD,

∴ ΔFBC ≌ ΔABD

∵ The area of ΔFBC is equal to (1/2)*FG² and the area of ΔABD is half of the area of BDLK.

∴ The area of BDLK is equal to FG². And then we can find the area of KLCE is equal to AH² with the same method.

∵ The area of BDEC = The area of BDLK + The area of KLCE.

∴ FG²+AH²=BD²

Conclusion

The Pythagorean theorem’s development has exerted a significant impact on mathematics. And this theorem gave us an idea to solve geometric problems with Algebraic thinking. It is also a great example about symbolic-graphic combination. This idea is very important for solving mathematical problems. By the Pythagorean theorem, we can derive a number of other true propositions and theorems, which will greatly facilitate our understanding of geometry problems, but it also has driven the development of mathematics.

Reference

[1] http://en.wikipedia.org/wiki/Pythagorean_theorem

[Fig.1] https://upload.wikimedia.org/wikipedia/commons/e/e0/ZhaoShuangRtTriangleGraph.PNG

[Fig.2]https://upload.wikimedia.org/wikipedia/commons/5/59/Illustration_to_Euclid%27s_proof_of_the_Pythagorean_theorem2.svg

Archimedes’ principle

Background of Archimedes

Archimedes was born in 287 BC into a wealthy family of nobility and his hometown was a small village near to Greece. He also had a great father who was a great astronomer and mathematician. His father was very friendly to his children, thus Archimedes was greatly influenced by his father. This made him take a keen interest in mathematics, astronomy and ancient Greek geometry when he was a child. In 267 BC, Archimedes was 11 years old. At that time, his father sent him to Alexandria, Egypt and let him learn mathematics with Euclid’s student. Alexandria, located in the mouth of the Nile, was the knowledge and cultural center of the world at that time. There were also a lot of scholars and professionals in various fields. During his stay in this city, Archimedes met many mathematicians, and he learned a lot of knowledge and skills from them. This knowledge made a major impact for his scientific career and is also the basis of his science research in the future.

Achievements of Archimedes

Fig.1 Archimedes’ principle. Image: Yupi666, via Wikimedia Commons.

Archimedes is considered by most great mathematicians as one of the greatest mathematicians of all time. And he had a lot of important achievements because of his early life of learning in Alexandria, Egypt. He was very good at learning, and this skill made him to find a way to solve areas, surface areas, volumes and other many geometrical objects. In addition to geometrical objects, he also had a important achievement in buoyant force. I think that Archimedes’ principle is his most important achievement. This principle told us the basic rule of buoyant force. According to Wikipedia, “the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces.”[1] We also can express this principle by using a formula such that F = G (F is the buoyancy and G is the weight of the liquid that the object displaces ). Another different expression is  (ρ is the density of liquid, g is the acceleration of gravity, V is the volume of liquid).

Story of Archimedes’ principle

Fig.2 Archimedes runs to the palace. Image: Public domain, via Wikimedia Commons.

According to legend, one day, the king of Greece asked his craftsman to make a gold crown for him. However, the king suspected his crown was not made of real gold after his craftsman completed the crown. The king was afraid that his craftsman pocketed his gold. Although the weight of the crown is equal to the weight of gold that he give to the craftsman, but he could not destroy the crown and check. This question stumped the king and his chancellor. At that time, Archimedes had a very good relationship with the king of Greece and he was already very famous in Greece. After he listened to the suggestion of his minister, the king was going to invite Archimedes to test the crown. In the beginning, Archimedes also had no idea how to solve this problem. One day, he was about to bathe in his bath tub. When he got into the bath tub and saw the water spill, he suddenly had a good idea to solve the king’s problem. He thought that he could measure the displacement of a solid in the water and use this method to determine if the crown was made of real gold. And then, he excitedly jumped out from bath tub and ran to the king’s palace. He even forgot to wear clothes and he said “Eureka! Eureka!” (Eureka means “Found it!”) When he arrived at the palace, he immediately began to test the crown. He put the same weight of pure gold and crown into the two bowls that filled with full water and to compare the water of overflow. Then he found that the bowl with real crown overflowed more water than another bowl. It means that crown was made of other metals. This proves that the craftsmen deceived the king. The significance of the test is not that whether the goldsmith deceive the king, but Archimedes discovered the Archimedes’ principle.

Conclusion

Archimedes’ principle is a very important theory for the world. We can see that many modern inventions were made by using this theory, like big ships, submarine and so on. Thus Archimedes was really a great scientist, and he has made an indelible impact for social progress and human development.

Reference

[1] http://en.wikipedia.org/wiki/Archimedes’_principle

Ancient Egyptian mathematics

Fig.1 Ancient Egyptian mathematics. Image: Ricardo Liberato, via Wikimedia Commons.

Egypt, located around the Nile, is one of the earliest developed culture areas in the world, and established a unified country near 3200 BC. The great characteristic of the Nile is the regularity of its floods. The periodic floods would inundate the whole land, which had to be re-measured when the waters receded. Egyptian mathematics developed to make accurate measurements for the division of land. In addition, mathematics also played an important role in prediction and preparation of flood events.

Fig. 2: Rhind Mathematical Papyrus. Image: Public domain, via Wikimedia Commons.

Our main awareness of Egyptian mathematics is based on two papyri, named the Moscow Mathematical Papyrus and the Rhind Mathematical Papyrus, which are preserved in Moscow and London respectively. Why were so few documents from ancient Egypt preserved? It’s because any kind of paper doesn’t last as long as stone, clay, or some other materials. The Egyptian utilized a kind of grass as “paper”, named papyrus, which looks like reeds and grows broadly around Nile Delta. However, this paper made of grass would easily dry and crack, and the records on it were really hard to preserve. Instead, some records on stone, clay, and other materials were preserved well. A Frenchman, whose name is Bastien, spent a very long time studying this information, and he finally figured out the meaning of the words on papyrus. His findings help us to understand some applications of the old mathematics on managing civil and religious matters. Specifically, the mathematics can be used in the division of land and wages, and the calculation of amounts of bricks required to build a building. In summary, the realistic problems motivated ancient Egyptians to master arithmetic operations, a fraction method and so on. We can see the ancient Egyptians had a gift in mathematics.

Fractions played an important role in ancient Egyptian mathematics. When an Egyptian conducted a fraction calculation, they only used as numerator. One of the famous examples in Egyptian fraction is how to divide bread. When ancient Egyptians divided nine loaves between ten people, instead of saying that each person should get 9/10 of a loaf, they would say each person should get 1/2+1/4+1/5+1/12+1/30 of a loaf. So why do they express fractions like that? According to Wikipedia, “An Egyptian fraction is the sum of distinct unit fractions, such as 1/2+1/3+1/16. That is, each fraction in the expression has a numerator equal to 1 and a denominator that is a positive integer, and all the denominators differ from each other. The value of an expression of this type is a positive rational number a/b; for instance the Egyptian fraction above sums to 43/48.[2]” We can see another bread example of how to divide only two loaves between three people. Firstly, they would divide two loaves to four halves, and each person would get half, the remaining 1/2 would be divided into three equal parts, and those three parts are divided between the three people. In the end, each person would get 1/2 plus 1/3 of 1/2, which sum is 2/3. Thus I think that they express fraction like this way because it was easy to understand for them. The Rhind Mathematical Papyrus also recorded some information about this method[3].

The origin of Egyptian mathematics was not as theory. Instead, the mathematics was applied to real life and to solve realistic problems. The beginning of mathematics was just a method to solve problems instead of a subject. Ancient Egyptian used mathematical methods to pay the workers, and found a way to pay them evenly. As time went by, people used this method and to improved this method. Thus, Egyptians studied mathematics and opened up a road for further development of mathematics. The ancient Egyptians not only invented the fraction, but also found other stuff. For example, the method of calculating area of a circle, their own calendar and so on. Those achievements brought great change and convenience for future life.

Reference:

[1]http://en.wikipedia.org/wiki/Ancient_Egyptian_mathematics

[2]http://en.wikipedia.org/wiki/Egyptian_fraction

[3]Clagett, Marshall Ancient Egyptian Science, A Source Book. Volume Three: Ancient Egyptian Mathematics (Memoirs of the American Philosophical Society) American Philosophical Society. 1999 ISBN 978-0-87169-232-0