When most people think of early mathematics, the first thing that comes to mind is probably Archimedes or Pythagoras of ancient Greece; or perhaps ancient Mesopotamia and its thousands of clay tablets, many of them containing math problems. Few people think of ancient Egypt. This is mainly due to the fact that little is known about ancient Egyptian math in comparison to these other civilizations. However, by looking at what we do know about Egyptian math and the feats of engineering they accomplished with it, we can recognize how complex and sophisticated it was.
A fragment from the Rhind Mathematical Papyrus. Image: Public domain, via Wikimedia Commons.
The majority of our knowledge of ancient Egyptian math comes from two papyri: the Rhind Mathematical Papyrus, which was originally written about 1985-1975 BCE; and the Moscow Mathematical papyrus, dating from around 1850 BCE. Math problems were not written on the walls of temples or great monuments in Egypt, so all math was probably done on papyrus or other perishable media, meaning that many mathematical works have not come down to us. This in in contrast to the mathematical documents from Mesopotamia, which were primarily done on clay tablets that are not as susceptible to the elements and ravages of time.
The ancient Egyptians probably developed the first base ten numerical system in human history. It was fully in use around 2700 BCE and perhaps even earlier. They had different symbols representing the powers of ten. A straight vertical line represented one, 10 was shown by a drawing of a hobble for cattle, a picture of a coil of rope served as a symbol for 100, a lotus plant delineated 1,000, a bent finger for 10,000, a tadpole or a frog for 100,000 and the picture of a god, perhaps Heh, represented 1 million. Although the Egyptian numerals were in a decimal system, it was not a positional place value system like the decimal system we use, or the sexagesimal (base 60) system developed by the Mesopotamians. Multiples of the powers of ten were written by repeating the symbol as many times as needed, and although they had a symbol for 1 million, other large numbers would have been very tedious to write. For instance, the number 987,654 would have required 39 characters. This Egyptian system possibly had an influence on the later Greek numerical system, but the Greeks improved upon it, creating a different symbol for each number 1-9, and other symbols for 20, 30 and so on.
Parts of the Eye of Horus were used to write fractions. Image: BenduKiwi, via Wikimedia Commons.
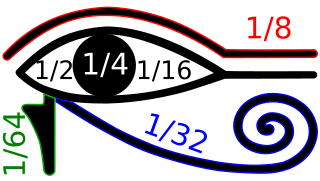
The Egyptians also had notation for fractions, although all Egyptian fractions were unit fractions (meaning they always had one in the numerator), with only two exceptions, 2/3 and 3/4. Fractions were marked by the hieroglyph for ‘R’ which is a long skinny oval, very similar in shape to the Eye of Horus. In fact, in an ancient Egyptian myth, the evil god Seth attacked his brother the god Horus and in the fight Seth gouged out the eye of Horus and tore it into pieces, fortunately the god Throth was able to put Horus’s eye back together and heal it. Thus, to honor the gods and this myth, whenever the Egyptians used fractions in relation to their measurement of volume, which is the hekat, the commonly used fractional parts were transcribed by using the corresponding parts of the Eye of Horus.
The great feats of engineering that the ancient Egyptians accomplished would have required an enormous amount of sophisticated math. The pyramids, for instance, are considered a marvel of mathematics and engineering. The base of the pyramids are almost perfect squares which the Egyptians would have achieved by using trigonometry, like the 3-4-5 trick. It was known in Egypt that a triangle with 3, 4 and 5 unit sides would always be a perfect right triangle. This Pythagorean triple, observed by the Egyptians long before Pythagoras, is sometimes called an “Egyptian triangle.” The Egyptians would have utilized this rule of geometry when laying out the base of a pyramid by tying knots in rope at 3, 4 and 5 unit intervals. Other tricks of trigonometry were known as well. The Rhind Mathematical Papyrus contains an equation for calculating the slope of a pyramid’s face, which is the same thing as finding the cotangent. It is also likely that they knew how to find a pyramid’s volume.
It is unfortunate that more is not known about the mathematics that were used by the ancient Egyptians, because they were obviously very skillful and innovative, and they must have been among the first people to develop important mathematical principals.
Sources:
http://discoveringegypt.com/egyptian-hieroglyphic-writing/egyptian-mathematics-numbers-hieroglyphs/
3010tangents 