Category Archives: Big Problems

Cryptography – Keeping Our Online Secrets Safe Since the 90s

A breakdown of time Americans spend with electronic media. Image: Courtesy of http://www.statista.com/chart/1971/electronic-media-use, Felix Richter

We live in an era where the internet is king. Between our cellphones, tablets, game consoles, laptops, and other devices, the average American adult (18+) spends 11 hours per day ingesting electronic media in some way, shape, or form. I’m sure we can all admit that on a weekly basis we access or create data that we don’t necessarily want the public to see. Whether it be our bank account or credit card information, our Facebook interactions, our emails, our tweets, our PayPal activity, or even our browsing history. That being said, I’m sure some of us take our internet privacy for granted; but how exactly does are internet privacy remain… private? The answer is simple: modular arithmetic. More specifically, cryptographic algorithms.

A History of Cryptography

Cryptography dates back to Egyptian scribes in 1900 B.C., and it was first used in their hieroglyphs. The Egyptians presumably wanted hide the content of their hieroglyphs from others, and they used very basic cryptography to do so. As you can imagine, this whole “keeping a message’s content safe” idea would become widely popular as mankind become more and more intelligent. The Romans, specifically Julius Caesar himself, created the first truly math-oriented cryptography. He used it primarily to protect messages of military significance. Caesar’s cryptographical ideas would later be used to build out modern day cryptography.

There are two main types of cryptography widely used across the web today: symmetric-key encryption, and asymmetric-key encryption (we’ll go into details later, I promise!). Both of these types of encryption rely on modular arithmetic. We must give credit where credit is due. Friedrich Gauss (1777-1855), birthed modular arithmetic in 1801. Believe it or not, this famous mathematician made most of his breakthroughs in his twenties! For those that aren’t familiar with modular arithmetic, here’s a timeless example (pun intended, wait for it…). The length of a linear line can have a start and end point, or it can go on to infinity in either direction. In modular arithmetic, the length of a “circular” number line is called the modulus. To actually do the arithmetic, consider this example: Take a regular clock (see, here’s the pun!), consisting of the numbers 1-12 . Clocks measure time on a 12 hour time table before starting back over at 1. The modulus for a 12-hour clock is 12 because it has 12 different numbers for the number of hours. To actually do the arithmetic, take this for example: It’s 8PM and we want to add 9 hours (8 + 9 mod 12). 8 +9 equals 17, however when using a modulus of 12, our number line wraps back around after counting to 12. For this we would count forward from 8 – ie. 8, 9 ,10, 11, 12, 1, 2, 3, 4, 5. So, (8 + 9 mod 12) = 5 AM in this case.

Caesar Cipher

A basic Caesar Cipher using a left shift of 3. Image: Matt_Crypto, via Wikimedia Commons.

As I said above, the Caesar cipher has acted as a building block for some of our modern day cryptography. Caesar’s main encryption step is incorporated in some of the more complex schemes we still rely on today. However, the Caesar cipher can be easily broken, or decrypted (more on this soon!). This particular cipher is concerned with the alphabet. The theory behind it is replacing each letter in the alphabet with a different letter some fixed number of positions down the alphabet (this is reffered to as the shift). For instance, with a shift of 3, A would replace D, and B would replace E.

Original: ABCDEFGHIJKLMNOPQRSTUVWXYZ

Cipher: XYZABCDEFGHIJKLMNOPQRSTUVW

This can be represented mathematically using modular arithmetic. The encryption of any letter ‘x” by a shift ‘n’ can be described as follows:

Encryption:

E(x) = (x + n) mod 26

Decryption:

D(x) = (x – n) mod 26

Brute-Force Attacking:

This cipher is extremely easy to break. There are only 26 possible shifts (26 different english letters). When taking a brute-force approach, it’s only a matter of varying through the different shifts until the message is decrypted. In fact, this process could be optimized by analyzing the encrypted string, finding frequently used letters and associating them with common vowels. That way, you could brute force using intelligent shifts. However, this approach would have to be modified when switching between languages.

Cryptography Online

As promised, I will explain the two types of internet cryptography. First, we have symmetric-key cryptography. This is based on the concept that both communicating parties share the same key for encryption as well as decryption. This key is mathematically applied to a numerical equivalent of the data each party is encrypting/decrypting. It is imperative that this key is kept secret. If another party finds out what the key is, none of the encrypted data is safe anymore. Symmetric-key cryptography uses either stream ciphers (encrypt the numerical representation of the data one digit at a time.), or block ciphers (taking blocks of digits, and encrypting them as a whole). Symmetric-key algorithms have an advantage over asymmetric in that they require less computational power.

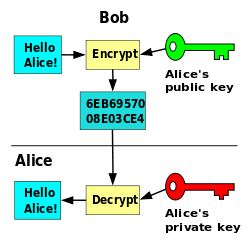
Asymmetric-Key encryption. Anyone can encrypt data using the public key, but the data only be decrypted with the private key. Image: Dave Gothenburg, via Wikimedia Commons.

As for Asymmetric-key cryptography (aka public-key cryptography) we use a slightly different approach. This cryptosystem implements both a private and public key. The public key is used to do the encryption (just like symmetric key cryptography), but the private key is used to do the decryption. The word “asymmetric” stems from the different keys performing opposite functions. This type of cryptosystem is more user friendly, and requires less administration. This is why public-key cryptography is widely implemented across the web.

The RSA Cryptosystem

The RSA cryptosystem is one of the most practical applications of modular mathematics we see today. In fact, if you look at your browser’s address bar right now and you see an “https” at the beginning of your URL, you’re more than likely relying on an RSA encryption to keep your data secure. RSA was created was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT. As far as cryptosystems are concerned, RSA in particular is one of the most straightforward to visualize mathematically. This algorithm consists of three parts: key generation, encryption, and decryption. I will be walking through a widely-used example using 3, and 11. Not only does this process use Gauss’s modular arithmetic, it also uses Euler’s totient function φ(n). (A function that counts the totatives of n – the positive integers less than or equal to n that are relatively prime to n.)

Generating the key is the most confusing part, but here’s a somewhat simplified version (don’t get nauseous!):

Randomly pick 2 prime numbers p and q : p=3 q=11
Calculate the modulus : n = p * q -> 3 * 11 = 33
Calculate the totient φ(n) : z = (p – 1) * (q – 1) -> ( 3 – 1) * (11 – 1) = 20
Choose a prime number k, such that k is co-prime to z : k=7
n and k become the public key
Calculate the private key : k * j = 1 mod z | 7 * j = 1 mod 20
In the previous step, we’re only interested in the remainder. Since we’re working with small numbers here, we can say –> 21/20 gives us “some number” with a remainder of 1. Therefore – 7 * j = 21 -> j = 3
j becomes the private key

After the public and private keys are generated, encryption and decryption become easy! Given P is the data we’d like to encrypt and E is the encrypted message we want to generate:

P^k = E (mod n) – When P (data we’d like to encrypt) = “14” We get: 14^7 = E mod 33 So E=20

Given E is the encrypted data we’ve received, and P is the data we want to decrypt:

E^j = P ( mod n) – 20^3 = P mod 33 So P = 14

This proves RSA works!

Does the RSA Cryptosystem Really Keep Me Safe?

Theoretically, a hacker could factor the modulus “n” in the steps above. Given the ability to recover the prime factors p and q an attacker can compute the “secret exponent” “d” from the public key (n, e). Once the hacker has this “secret exponent”, they can decrypt all data sent with its matching public key. RSA keeps us safe from hackers because there is no known algorithm (The NSA probably has one!) that can factor these large integers in a timely manner. In fact, the largest known number ever factored was 768 bits (232 digits!) long, and this was done with a supercomputer using a state-of-the-art implementation. If that doesn’t make you feel safe enough, RSA keys are typically 1024 to 2048 bits (617 digits!) long, so we don’t need to worry about our data getting hijacked. However it is recommended that we use a value of n that is at least 2048 bits long to ensure the encryption is never cracked.

Sources:

http://en.wikipedia.org/wiki/RSA_(cryptosystem)

http://blogs.ams.org/mathgradblog/2014/03/30/rsa/

http://www.studentpulse.com/articles/41/a-brief-history-of-cryptography

http://www.ti89.com/cryptotut/mod_arithmetic.htm

http://en.wikipedia.org/wiki/Modular_arithmetic

http://cunymathblog.commons.gc.cuny.edu/

How and Why RSA works:

https://www.youtube.com/watch?v=wXB-V_Keiu8

Code Breaking: Bletchley Park and Bill Tutte

While brainstorming ideas for a blog post, I found myself wondering if math has ever directly saved lives. After looking into many options, I ran into a story about a place called Bletchley Park. It was known as the Fortress of Secrets and was said to have saved millions of lives yet didn’t even appear on any map. Nicknamed ‘Station X,’ it was solely designated for breaking codes, specifically ciphers. In World War II, direct communication between leaders and various units around the world was a big problem. These orders/war plans were coded and broadcast via wireless radio, but because they could be so easily intercepted, they became increasingly vulnerable. The solution to this problem was the cipher machine. Adopted in 1926, the Germans’ answer was called the Enigma.

A Lorenz machine. Image: Public domain, via Wikimedia Commons.

The Enigma was thought by the Germans to be unbreakable and safe for them to use. Its code was especially hard to crack because each time a key was pressed, its internal wiring was changed. In light of this, the British started to recruit brilliant mathematicians to engage in a battle to learn the enemy’s secrets. The Enigma machine required 6 people to operate, so Hitler ordered even more security. Thus, the Tunny cipher machine was born (also known as the Lorenz Machine). This machine generated code with its 12 wheels and only required two operators to send and receive information. To function, it would first apply two keys, encoding the message twice. The first cipher used 5 wheels with, the second used another 5, and then 2 additional wheels would cause a stutter of random letters that would try to throw off unauthorized decoders. Each wheel had a different number of spokes or choices on it which resulted in 23*26*29*31*37*41*43*47*51*53*59*61 = 1.6 million billion possible combinations!

Here is an example of coding one letter into another: The initial letter is “A,” and the cipher code is “K.” They would be “added up,” and if the corresponding symbol was different, then you would mark down an “x.” Inversely, if it was the same, then you would mark down a *. Here we can see A being coded into the letter N:

A= x x * * *

K= x x x x *

———————–

* * x x * = N

The code’s downfall began with the Germans’ overconfidence in the Tunny machine. A 4000 character message was sent, but the receiver didn’t quite get it, so a re-send was requested. The sender failed to change the wheel settings and re-sent the 4000 character message but it was slightly different. This provided Bletchley with a data set with which he could attempt to crack the code. John Tiltman, a mathematician who led the research department at Bletchley, initially worked on this break but passed it onto Bill Tutte.

Bill began by putting the 4000 word message into columns and made a rectangle out of it. He then looked for repetitions/patterns. Every 23 characters there was a rotation, but he then thought maybe it was 25. So he tried to multiply 23*25 to see if the pattern extends along that but it was inconclusive. But the pattern did extend along 574. He then thought maybe it was 41 as that is the prime number of 574. Resonance occurring after 41 strokes made him deduce that the first wheel had 41 spokes. He then went to the next wheel and so forth. Bill Tutte managed to diagnose how the machine worked without ever actually seeing the machine.

He also worked out a statistical mathematical method of breaking the Tunny code, called the “1+2 – break in method.” To use this decoding method required a massive amount of number-crunching and checking. This is where his co-worker Thomas Flower’s brilliance came into play. He conceptualized Bill Tutte’s method and produced one of the first computers, The Colossus, the world’s first semi-programmable computer completely invented from scratch. With this cracked code—and the computer to help crack it—huge battles were won. It is widely credited with turning the tide of the entire war.

World War II is estimated to have cost 10 million lives per year. Cracking the Tunny code was said to have shortened the war by at least two full years! However, everything involving these machines and ciphers had to be kept secret. The brilliant men involved could not publicly get credit for their achievements for quite some time. Eventually, the secrets were declassified, and Bill Tutte was awarded a membership of the Royal Society. In 1987, he finally signed his name in the Royal Society book where his signature lies alongside those of Isaac Newton, Charles Darwin, Winston Churchill.

Sources:

BBC Documentary: http://vimeo.com/31185786

http://www.bletchleypark.org.uk/content/hist/worldwartwo/enigma.rhtm

http://www.bbc.com/news/uk-england-suffolk-29064159

http://www.english-heritage.org.uk/bletchleypark

-1 x -1 = 1, but why?

The product of two negative numbers produces a positive number. Did it ever make you wonder why? The sum of two negative numbers is still negative, but why positive when multiplied? Come to think of it, how is it even possible to multiply a negative number by a negative number?

One of the easiest ways to understand the concept of negative number is to think of gain as positive, and loss as negative. This way may explain addition and subtraction, but when it comes to multiplication and division, it gets confusing. Stendhal, a French writer famous for his novel The Red and the Black, says in his autobiography, “suppose the negative quantities are a man’s debts, how by multiplying 10,000 francs of debt by 500 francs, will he or can he manage to acquire a fortune of 5,000,000, five million?” He puzzled over the improbable conversion or “changing sides” across a horizontal boundary in the image below.

Stendhal, quite the intellect of the age himself, shows that there were souls who agonized over this conceptual problem. As a matter of fact, the concept of a negative number was formally introduced much later than the concept of an irrational number in Europe, which might mean that people were more comfortable with operations on the latter than on the former. Math historian Ronald Calinger writes that even Blaise Pascal “derided those who thought of taking four away from nothing and getting minus four.”

In the 7th century, Indian mathematician Brahmagupta first discovered that a minus times a minus equals a plus, but even after a thousand years there were dissenting voices. In 18th century Europe many scholars overtly argued against it on the basis of reasoning that’s like “-3 is smaller than 2, then how can square of -3 be greater than square of 2?” So we can imagine the resistance that the concept of negative number created among people.

Model of positive and negative: gain and loss

Like Stendhal did, there is a model of gain and loss to represent the concept of signs. Adding a positive number would be gain, or profit, and adding a negative number (subtracting positive number) is loss. When gain becomes less than zero, it is interpreted as debt. We human beings, by our very nature, tend to apply the same thinking mechanism that was once successful again and again even in different circumstances, so it is natural for us to try to understand the multiplication and division under the same logic.

Then why is it inappropriate when operating on multiplication?

Do not multiply debt by debt

We realize that explaining multiplication of positive numbers by using the model does not make sense even before we get to negative numbers. Does multiplying gain by gain produce gain? When we have 10 of 100 dollar (bills), it means we have 1,000 dollars. (10 x 100 = 1,000.) It sounds perfectly reasonable according to the example. However, units are different; 100 is in dollars while 10 is a number of bills. We could interpret each 100 dollars as gain, but 10 is in a different unit of gain. It may be a contextually valid statement, but in mathematical sense, it is flawed because the unit of 10 simply disappears in the result.

The statement that gain times gain is gain may be invalid, but the model itself has no problem explaining that a plus times a plus equals a plus if we ignore the measurement issue and only consider the contextual interpretation. In addition, it can also explain a minus times a plus equals a minus. For example, when there are 10 people who owe you 100 dollars, you know they owe you 1,000 dollars as a whole. -100 x 10 = -1,000

But the model’s biggest drawback is that it cannot explain a minus times a minus even in a contextual sense because there is no measurement to quantify a negative number of, well, people, and things.

Then, how can we understand that a minus times a minus equals a plus?

1. Finding a pattern

The rows tell us that each product changes by the same amount when the number on the right gets smaller. The columns also show the same pattern: the first column decreases by 2, the second by 1, the third by 0, the fourth column increases by 1, and the fifth by 2. Accordingly, the next row would be,

From this, we learn that a minus times a minus produces a plus.

2. A horizontal line

One of the basic approach to negative number is giving the number a direction. It is to associate positive and negative number with positive direction and negative direction, so they move in the opposite way on a horizontal line. 3 and -3 are apart from the origin by the same distance, but their opposite directions make them different numbers. In fact, people finally stopped resisting the concept of signs when the horizontal line model was introduced. For example, multiplying 2 by 3 is adding three 2’s, so it is like moving by the amount of 2 three times from zero to the right on the line, which equals to 6. In a similar sense, multiplying 2 by -3 is moving by 2 from zero to the left (opposite direction of 2) three times.

It is the same as thinking of moving by -2 three times (the direction of -2), which tells that 2 x (-3) = (-2) x 3.

Finally (-2) x (-3) is moving by -2, yet in the opposite direction of (-2) three times, which basically cancels out and happens to move to the right. It leads to our desirable conclusion (-2) x (-3) = 6.

3. Gain and loss model revisited

We can explain multiplication of negative numbers by expanding the rules of the model. We include negative number operations beside the positive ones. Adding a negative number means decreasing gain, or increasing loss, or debt. Subtracting a negative number means decreasing loss, or debt, in other words, increasing gain. So for example, when a is a positive number, subtracting (-a) means that debt is decreased by the amount of a, so gain is increased by a. In short, -(-a) equals a, and from the model, we can logically justify that (-a) x b = -(a x b) = a x (-b) when a and b are positive. Then let’s say b is a negative number. We can express b equals -c for some positive number c. By substitution, (-a) x (-c) = a x (-(-c)) = a x c.

Thus, a negative number times a negative number is a positive number.

4. Mathematical proof

I explained that a minus times a minus equals a plus, but technically it wasn’t a proof. To prove (-a) x (-b) = ab, I will use the associative law of addition, the distributive law of addition and multiplication, and the fact that zero is the identity element under addition. We know 0 = 1+ (-1). Multiply both sides by -1, and apply the distributive law.

0 = (1+ (-1)) x (-1)

= 1 x (-1) + (-1) x (-1)

Since 1 x (-1) = -1, the equation above become 0 = -1 + (-1) x (-1). Add 1 to both sides, and we get 1= (-1) x (-1).

The formal proof will follow this format. But before I do that, I will show 0 x b =0.

0 = 0 x b – (0 x b)

= ((0+0) x b) – (0 x b)

= (0 x b + 0 x b) – (0 x b) = 0 x b

Without the loss of generality, a x 0 = 0 is true.

Now I want to show (-a) x (-b) = ab

(-a) x (-b) – a x b = (-a) x (-b) + a x (-b) – a x (-b) – a x b

= ((-a) + a) x (-b) – (a x (-b) + a x b)

= 0 x (-b) – (a x (-b + b))

= 0 – a x 0 = 0 – 0 = 0

QED

Stendhal, The Life of Henry Brulard, trans. John Sturrock (New York: NYRB, 2002), 364-66.

Calinger, Ronald. Vita Mathematica: Historical Research and Integration with Teaching (New York: Cambridge University Press, 1996), 36.

http://nonsite.org/article/overlooking-in-stendhal

Imaginary Numbers: From Outcast to Respectability

My infinity is bigger than your infinity

1 Reply

When I was a child, I purposely found something to think about to help me fall asleep. Usually I picked cartoons or super powers, but sometimes things just came into my head, like it or not. What was the worst? Thinking about heaven. At first, heaven seems all right. There is a lot to do, gold everywhere (though no purpose for it), people are nice (it’s a prerequisite), you get to see most of your family, and there is plenty to eat (though no one is ever hungry). Anyway, I start thinking about FOREVER.

At first, it is just a sensation; a weird sensation like tingling and falling and nothingness. It is not a sensation that I can make sense of really because forever doesn’t really make sense, at least not to a 10 year old. I try to get away from forever but forever is a huge part of the definition of heaven. Then, the opening credits of the Twilight Zone, with the music, and starry sky, usually appear. Fade to myself standing, looking at heaven, in the dressing room mirrors of infinity. You know, when dressing rooms have those three mirrors that are angled just perfectly so the images are smaller and smaller replicas of one another, on and on, into infinity. This picture, and thoughts of the foreverness of heaven, kept me up at night as a child.

I am glad to say that forever no longer keeps me up at night. While I still find no comfort in the foreverness of heaven, the lack of a middle ground between forever and my time on earth is what usually keeps me up at night now. However; I still can’t stand it when mirrors are angled that way. It creeps me out, and I can’t help but wonder if there is an end, or if I can find a flaw from one image to the next. In my opinion, we are not meant to look into infinity like that, squarely.

When beginning to pursue mathematics, I thought math might clarify, or in some way define, forever (or as adults call it, infinity). On the contrary, Math has actually made it stranger. Theories in math have shown numerous types of infinity, and infinities within infinities, and sizes of infinities, and calculations of infinity. None of this brings me any comfort, except to say that we obviously don’t have this figured out yet because that is just not possible. Infinity is infinity, and it is very large, incalculable and non-denumerable, and there is only one kind; it is called forever. Heaven can only exist in one, all-encompassing infinity.

When reading A History of Mathematics, I read about Zeno’s paradox. That led to an internet search, and then to Numberphile. I watched the video, accepted the idea, and left it alone. The solution seemed reasonable enough. Later in the semester, I was required to do a research project. By some unknown scheme, we picked Georg Cantor, whom I had never heard of. If you haven’t either, he is the creator of set theory but also perhaps the mathematical or scientific father of infinity. You just can’t shake things off in life. They follow you.

My research for that project led me to question the mathematical view of infinity. Let me start by saying, I know very little of Math’s view of infinity. It seems to be an infinite topic. This is where I am in my understanding – so please comment, post, reply, educate me, and critique my understanding. Calculus one is a prerequisite for the course, and being a rule follower, I have that. So, I had experience computing limits to infinity. That is relatively easy. BUT, those are just numbers. They aren’t real things. Numbers aren’t real. So, of course I could compute the infinity of something that isn’t really real. What numbers represent is real; like Zeno’s paradox. Zeno’s paradox applies numbers to something real – something actually happening in the world (theoretically). In other words, when I take the limit of a sequence that goes to infinity, it has no relation to time or space. It is just numbers. But, if I were taking the limit of Zeno’s paradox to see how far Zeno actually travels, or to find the time it takes to travel, or to see if he can ever catch the turtle, I would have to do so in relation to time and space. When I do that, the exact opposite answer occurs. Zeno will never catch the turtle. That mathematics isn’t computing real infinity or perhaps all of infinity is perhaps echoed by the Numberphile narrator when he asks, “What I want to ask a physicist is, can you divide space and time infinitely many times?” Similarly, Kelly MacCarthur wonders in the Calculus 2 video used for online math courses, “Can I take infinitely many steps?”

However, if all of space and time existed at one instant, forever, then Math has it right. It could calculate the infinite because it occurs all at once. There is no sequence, event after event – in essence, no time or space really because it is all at once, everywhere. Yes, there are scientific theories, philosophies, and religions which believe this is the case. Of course, this idea is contrary to most people’s understanding of infinity. Whenever math instructors talk about infinity, they always say, “Infinity is only a concept. It is not a number.” Yes, it is only a concept but is it also something real? If it is only a concept then why are we computing something real that is a concept? Why would we bother to compute a concept? It seems like Math is walking a funny line here.

Math has worked something out though. I’m just not sure what it is. Math is summing an infinite process (as if infinity happened to end). Obviously, Math’s understanding of infinity has proven useful in mathematical calculations and many practical applications. To paraphrase others before Cantor, “It works. So, no need to define it. It works.” So, Math has worked something out about infinity but what has Math worked out, and is it really infinity?

Mathematicians always like to joke about engineers rounding numbers to 3 or 4 places because it doesn’t really matter to engineering after that, but is mathematics rounding off infinity or at least only capturing some aspect of infinity? After all, how can there be different types of infinity? My preferred illustration for the existence of multiple infinities is from Galileo. Galileo used a thoughtful but intuitive approach to understand infinity. He drew a circle. Then, he drew an infinite number of rays from the center of the circle. These rays filled up the space inside the circle. But then, he drew a larger circle around the smaller one and extended those rays to the larger circle. Though he drew as many rays as possible (an infinite number perhaps), the infinite number of rays did not fill up the larger circle; there were spaces between the rays. This led him to believe that first infinity was not large enough for the second circle; not even close. He would need another size of infinity to fill up the larger circle. [BAM! PHH! Did your mind just explode?] It is important to note that intuitively, his illustration makes sense. However, with today’s current understanding of infinity and better ability to calculate infinity, we now know that the infinity in the smaller circle leaves no space between the rays when extending to a larger circle. But, I liked his intuitive approach. Though intuition seems to be severely lacking when it comes to infinity.